Diese Briefstelle ist von historischer Bedeutung, vergleichbar etwa mit dem Brief Artins vom 17.Juli 1927 (Nr.8), in welchem er über den Beweis des allgemeinen Reziprozitätsgesetzes berichtete. Wir werden Zeuge einer neuen Wendung in der bewegten Geschichte der Klassenkörpertheorie. Es geht um eine Neufassung der Grundlagen, auf denen das Artinsche Reziprozitätsgesetz fußte. Diese Grundlagen waren von Weber, Hilbert, Furtwängler und Takagi geschaffen worden und in übersichtlicher Form systematisch im 1.Teil des Hasseschen Klassenkörperberichts dargestellt [Has26a]. Obwohl die Hassesche Darstellung sehr begrüßt worden war, so war doch ein allgemeines Unbehagen entstanden über die Diskrepanz zwischen der einfachen und übersichtlichen Form, die die Hauptsätze der Theorie angenommen hatten, und deren verschlungenen und teilweise komplizierten Beweisen. Hasse selbst hatte verschiedentlich auf diese Diskrepanz hingewiesen und auf die Notwendigkeit, die Klassenkörpertheorie einfacher zu begründen. (Vgl. 12.1.) Dies wurde nun durch die „ungeheuren Vereinfachungen“, von denen Artin spricht, in Angriff genommen.
Schon früher einmal gab es einen Gedankenaustausch zwischen Artin und Hasse über eine mögliche Vereinfachung des Aufbaus der Klassenkörpertheorie. Wir verweisen dazu auf den Brief Nr.12 vom 29.7.1027 und die darauf folgenden Briefe. Der Enthusiasmus, der in dem vorliegenden Brief zum Ausdruck kommt, kann gedeutet werden als Ausdruck der Genugtuung, dass es endlich gelungen ist, ein Stück weiter zu kommen.
Man muss jedoch im Auge behalten, dass dies noch nicht zu einem endgültigen Ergebnis führte. Es handelte sich um einen von mehreren Schritten auf dem Weg zum Verständnis der Klassenkörpertheorie; erst die Ergebnisse von Chevalley im kommenden Jahrzehnt der 1930er Jahre werden in gewisser Weise als abschließend bezeichnet werden können; sie lieferten die Grundlage, auf der sich dann die weitere Entwicklung abspielte, mit den Methoden einerseits der Kohomologie und andererseits der arithmetischen Geometrie.
Die jetzt erreichte neue Wendung wird gewöhnlich Herbrand und Chevalley zugeschrieben [CH31]. Aus dem vorliegenden Brief ersehen wir, dass auch Artin daran beteiligt war. Er spricht zwar davon, dass dies nur an „einigen kleinen Punkten“ geschehen ist, aber wie wir Artin kennen, wird sein Einfluss dabei nicht klein gewesen sein. Zumindest der Teil, den er in seinem Brief mit „analytisch“ bezeichnet, wurde wesentlich von ihm selbst gestaltet. Sein Enthusiasmus hat sicherlich viel dazu beigetragen, dass die neue Wendung unter den Zahlentheoretikern schnell bekannt wurde. (Vgl. dazu 39.2.)
Herbrand war im Juni 1931 als Rockefeller-Stipendiat zu Artin nach Hamburg gegangen. (Vgl. 39.3.) Offenbar hatte er im Artinschen Seminar über seine Ergebnisse berichtet, die er zum Teil in Kooperation mit Chevalley111 gewonnen hatte. Gleich nach der Abreise von Herbrand aus Hamburg informiert nun Artin seinen Briefpartner Hasse über die neue Entwicklung, noch ganz unter dem unmittelbaren Eindruck dieser Ergebnisse. Die Sachen sind offenbar noch nicht vollständig aufgeschrieben; Artin skizziert sozusagen freihändig mit großer Geste, wie er sich den neuen Aufbau vorstellt.
Wenn man die Ausführungen Artins im vorliegenden Brief verstehen will, so hat man diese im Kontext von Hasses Klassenkörperbericht Teil I [Has26a] zu lesen. Dieser Bericht war damals nicht nur die Quelle für die jungen Mathematiker geworden, die die Klassenkörpertheorie lernen wollten (z.Bsp. Herbrand und Chevalley), sondern er wurde auch allgemein als Referenz benutzt, wenn man nicht unbedingt die früheren Arbeiten von Takagi, Weber, Furtwängler usw. zitieren musste. Wir werden ihn im folgenden kurz mit „Bericht“ zitieren.
Zunächst geht es um die sogenannte 1.Ungleichung
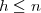
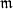 . Die
einzige Bedingung ist, wie Artin sagt, dass
. Die
einzige Bedingung ist, wie Artin sagt, dass
H alle Idealnormen aus K enthält.
Gemeint sind natürlich die Relativnormen der zu 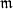 teilerfremden Ideale
von K.
teilerfremden Ideale
von K.
Im „Bericht“ findet sich die 1.Ungleichung gleich zu Beginn in §5, Satz 8. Dort werden zwar nur galoissche Körpererweiterungen behandelt, während jetzt Artin ausdrücklich sagt, dass K|k nicht galoissch zu sein braucht. Aber diese Verallgemeinerung ist wohl nicht als der wesentliche Fortschritt zu bezeichnen. Wesentlich ist, dass jetzt gleichzeitig das
mit herauskommt, falls  nicht der Hauptcharakter ist. Es verwundert einigermaßen,
dass dies nicht auch schon im „Bericht“ an dieser Stelle erwähnt wird, denn die
Schlussweise von Artin hier ist genau dieselbe wie die von Hasse dort. Das ist in
der Mathematik nicht selten zu beobachten: die sorgfältige Durchmusterung der
verwendeten Schlussweisen kann oft zu nützlichen Verallgemeinerungen oder
Vereinfachungen führen.
nicht der Hauptcharakter ist. Es verwundert einigermaßen,
dass dies nicht auch schon im „Bericht“ an dieser Stelle erwähnt wird, denn die
Schlussweise von Artin hier ist genau dieselbe wie die von Hasse dort. Das ist in
der Mathematik nicht selten zu beobachten: die sorgfältige Durchmusterung der
verwendeten Schlussweisen kann oft zu nützlichen Verallgemeinerungen oder
Vereinfachungen führen.
Es handelt sich um die klassischen Weberschen L-Funktionen
der Zahlentheorie (also nicht um die neuartigen Artinschen
L-Funktionen, die in den Briefen vom vergangenen Jahr zur Sprache
kamen112 ).
Diese L-Funktionen L(s, ) gehören also zu den Charakteren
) gehören also zu den Charakteren  der Faktorgruppe
A/H (dabei bezeichnet A die Gruppe der zum Modul
der Faktorgruppe
A/H (dabei bezeichnet A die Gruppe der zum Modul 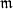 teilerfremden Ideale).
Artin schreibt die L-Funktion als e-Potenz und arbeitet mit dem Exponenten,
d.h. er arbeitet mit dem Logarithmus (in geeigneter Normierung)
teilerfremden Ideale).
Artin schreibt die L-Funktion als e-Potenz und arbeitet mit dem Exponenten,
d.h. er arbeitet mit dem Logarithmus (in geeigneter Normierung)
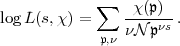
Dabei durchläuft  die zu
die zu 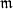 teilerfremden Primideale und N bedeutet die
Absolutnorm. s > 1 bezeichnet stets eine reelle Variable, und im vorliegenden
Zusammenhang kommt es auf den Grenzübergang s
teilerfremden Primideale und N bedeutet die
Absolutnorm. s > 1 bezeichnet stets eine reelle Variable, und im vorliegenden
Zusammenhang kommt es auf den Grenzübergang s  1 an.
1 an.
Artin hält sich nicht damit auf, die Reihe für log L(s, ) hinzuschreiben; er
konnte eben voraussetzen, dass Hasse mit den Begriffsbildungen und der ganzen
Situation vertraut war. Er nimmt das Produkt der L-Funktionen zu den
verschiedenen Charakteren
) hinzuschreiben; er
konnte eben voraussetzen, dass Hasse mit den Begriffsbildungen und der ganzen
Situation vertraut war. Er nimmt das Produkt der L-Funktionen zu den
verschiedenen Charakteren  ; im Exponenten bedeutet das die Summe der
Logarithmen. Diese Summe ergibt aufgrund der Charakterrelationen:
; im Exponenten bedeutet das die Summe der
Logarithmen. Diese Summe ergibt aufgrund der Charakterrelationen:
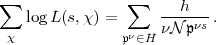 | (48) |
Die rechte Seite schreibt Artin hin. Dies ist eine Doppelsumme über alle Paare
 ,
, für welche
für welche 

 H ist.
H ist.
Dies wird nun verglichen mit der Zetafunktion des Oberkörpers K:
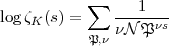
wobei 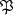 die Primideale von K durchläuft. Im vorliegenden Zusammenhang
kommt es nur auf das Verhalten für s
die Primideale von K durchläuft. Im vorliegenden Zusammenhang
kommt es nur auf das Verhalten für s  1 an, und man kann eine für s
1 an, und man kann eine für s  1
beschränkte Funktion beliebig hinzufügen oder weglassen. Aus diesem Grund
kann man diejenigen Terme auf der rechten Seite weglassen, für welche
1
beschränkte Funktion beliebig hinzufügen oder weglassen. Aus diesem Grund
kann man diejenigen Terme auf der rechten Seite weglassen, für welche 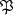 vom
Relativgrad > 1 ist. Für jedes Primideal
vom
Relativgrad > 1 ist. Für jedes Primideal  von k erscheinen somit auf der rechten
Seite m
von k erscheinen somit auf der rechten
Seite m Terme, wobei m
Terme, wobei m (von Artin mit m bezeichnet) die Anzahl der
Primteiler
(von Artin mit m bezeichnet) die Anzahl der
Primteiler 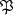 |
| vom Relativgrad 1 ist. Bezeichnet MK die Menge der Primideale
vom Relativgrad 1 ist. Bezeichnet MK die Menge der Primideale

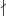
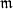 von k, für welche m
von k, für welche m > 0, so folgt also
> 0, so folgt also
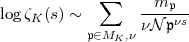
Hier benutzen wir die von Hasse eingeführte Schreibweise ~ welche besagt,
dass die Differenz beider Seiten eine für s  1 beschränkte Funktion
ist.
1 beschränkte Funktion
ist.
Nun benutzt Artin die Voraussetzung, dass H alle Relativnormen
aus K enthält, insbesondere also alle 
 MK. Also kommt für jedes
MK. Also kommt für jedes

 MK ein Term auch in (48) vor, und wegen m
MK ein Term auch in (48) vor, und wegen m < n ergibt sich die
Abschätzung
< n ergibt sich die
Abschätzung
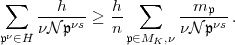 | (49) |
Diese so einfach herzuleitende Relation (49) findet sich, wie schon gesagt, bereits im „Bericht“ (§5, 3.), wenn dort auch nur für galoissche Erweiterungen ausgesprochen.113 Was neu ist, das sind die Folgerungen, die Artin hieraus zieht. Nämlich:
Da die rechte Seite in (49) für s  1 gegen +
1 gegen +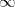 divergiert (weil
divergiert (weil  K(s) an der
Stelle s = 1 einen Pol besitzt), so auch die linke Seite in (49), also auch die linke
Seite in (48). Mithin hat das L-Reihenprodukt
K(s) an der
Stelle s = 1 einen Pol besitzt), so auch die linke Seite in (49), also auch die linke
Seite in (48). Mithin hat das L-Reihenprodukt
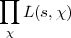
an der Stelle s = 1 einen Pol, , d.h. der für den Hauptcharakter  = 1
auftretende Pol 1.Ordnung kann sich nicht durch eine Nullstelle einer der anderen
L-Funktionen herausheben. Es ist also
= 1
auftretende Pol 1.Ordnung kann sich nicht durch eine Nullstelle einer der anderen
L-Funktionen herausheben. Es ist also
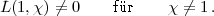 | (50) |
Über diese Beobachtung ist Artin so erfreut, dass sie ihm die Exklamation „Bitte!“ entlockt. Und er sagt dazu, dass er überhaupt nicht die Fortsetzbarkeit der L-Funktionen benötigt114 , sondern lediglich die Regularität bei s = 1.115 Er sagt allerdings nicht, wie er sich den Beweis der Regularität ohne die Fortsetzbarkeit vorstellt.
Was diese Regularität anlangt, so wird sie in dem „Bericht“ nicht
bewiesen, sondern es wird nur auf eine alte Arbeit von Weber aus
dem Jahr 1897 verwiesen [Web97], mit einem Hinweis, dass und
wie man evtl. die dortigen Beweise in eine moderne mathematische
Schreibweise übersetzen könne. Artin selbst sagt in seinen Göttinger
Vorträgen116 ,
dies erfordere eine „ziemlich komplizierte“ Überlegung. Erst in den Hasseschen Marburger
Vorlesungen117
finden wir einen ausführlichen Beweis, basierend auf den einschlägigen
Abschätzungen der Koeffizientensummen der Dirichletschen Reihenentwicklungen
für die L-Funktionen (diese sind noch in einem gewissen Bereich s > 1 -  konvergent, aber nicht mehr absolut, d.h. es kommt auf die Reihenfolge der Terme
an).
konvergent, aber nicht mehr absolut, d.h. es kommt auf die Reihenfolge der Terme
an).
Immerhin sagt Artin in dem vorliegenden Brief an Hasse, dass ja die Regularität der L-Funktionen bei s = 1 schließlich die „übliche Annahme der Klassenkörpertheorie“ sei, insofern sei also seine Überlegung nicht komplizierter als die übliche. Und er sagt auch, dass seine Überlegung „ohne Frobenius“ gehe, d.h. ohne auf den Dichtigkeitssatz von Frobenius (oder gar den von Tschebotareff) zurückzugreifen.
Nun aber: Da das Nichtverschwinden der L-Reihen (50) gesichert ist, ergeben sich sofort eine ganze Reihe von Folgerungen, die für den Aufbau der Klassenkörpertheorie von entscheidender Bedeutung sind. Es sei betont, dass dies keine neuen Resultate waren; die von Artin angegebenen Sätze waren innerhalb der Klassenkörpertheorie wohlbekannt. Es geht Artin darum, in welcher Reihenfolge diese Sätze bewiesen werden, also um das Schema eines neuen Aufbaus der Klassenkörpertheorie.
Wenn h = n ist, wenn also K|k ein Klassenkörper nach der Takagischen Definition ist, dann, so folgert Artin, zerfallen fast alle Primideale aus H vollständig in K, d.h. alle bis auf eine evtl. Ausnahmemenge der Dichte 0. Gemeint ist dabei natürlich die sog. Dirichlet-Dichte. Davon gilt auch die Umkehrung. Diesen Satz formuliert Hasse in seinen Marburger Vorlesungen als „Satz von Artin“ 118 . Daraus können wir wohl schließen, dass dieser Satz in der Tat von Artin stammt, und also nicht von Herbrand und/oder Chevalley. Und dieser Satz von Artin spielt eine wichtige Rolle beim Aufbau der Klassenkörpertheorie. In einem späteren Stadium des Aufbaues stellt sich dann heraus, dass der Satz dahingehend präzisiert werden kann, dass wirklich alle Primideale aus H vollständig zerfallen in K.
Hier bezieht sich Artin auf das Beweisschema in dem „Bericht“, mit dem er das neue Beweisschema vergleicht. Auch dort gibt es eine Reihe von Beweisschritten, die von Hasse „Reduktionen“ genannt worden waren.
Artin unterscheidet 2 Reduktionen:
1) Der „Umkehrsatz“ besagt, dass jede abelsche Erweiterung ein Klassenkörper ist. Weil Artin soeben schon den Satz über Körperkomposita bewiesen hat, so braucht der Umkehrsatz nur für zyklische Erweiterungen K|k bewiesen zu werden. Und für zyklische Erweiterungen, so sagt er weiter unten, reduziert sich der Umkehrsatz auf die Bestimmung zweier Gruppenindizes. Das ist wie früher im „Bericht“. Neu aber ist, dass sich jetzt die Berechnung dieser Indizes, wie Artin sagt, „in zwei Zeilen“ durchführen läßt. Zwar sind diese „zwei Zeilen“ wohl etwas übertrieben (oder besser: untertrieben), aber Tatsache ist, dass sich in der Tat diese Berechnung jetzt sehr viel einfacher gestalten lässt als früher. Und zwar sofort für beliebige zyklische Erweiterungen, während im „Bericht“ zunächst per Induktion auf den Fall eines Primzahlgrades zurückgeschlossen und der Beweis in diesem Falle mit dem Beweis des Existenzsatzes verwoben werden musste. Dies ist der „ungeheure Fortschritt“, von dem Artin eingangs gesprochen hat, und der auf Herbrand und Chevalley zurückgeht. Der gruppentheoretische Hilfssatz, von dem Artin spricht, ist heute unter dem Namen „Herbrandsches Lemma“ wohlbekannt und wird meist als Aussage über die Kohomologie zyklischer Gruppen interpretiert.
Jedoch verliert Artin hier kein Wort über die Natur dieses Hilfssatzes. Das wäre doch vielleicht informativ für Hasse gewesen, insbesondere weil es, wie Artin anmerkt, doch die „schlimmen Rechnungen“ unnötig machte.119
Als Resultat dieser Indexrechnungen kommt heraus, wenn K|k Klassenkörper zu H ist, dass dann
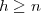
ist, also die sogenannte 2.Ungleichung der Klassenkörpertheorie. Im zyklischen Falle ergibt sich noch als Nebenprodukt das Lokal-Global-Prinzip für die Normen – jedenfalls, wenn man die lokale Klassenkörpertheorie voraussetzt. Wir beachten, dass die Entdeckung der lokalen Klassenkörpertheorie durch Hasse und F.K.Schmidt bereits mehr als ein Jahr zurückliegt [Has30c]; damals jedoch musste noch die globale Klassenkörpertheorie zum Aufbau der lokalen Klassenkörpertheorie benutzt werden. Erst ein weiteres Jahr später gelang es Hasse, angeregt durch Emmy Noether, die lokale Klassenkörpertheorie ohne Benutzung der globalen zu begründen.
2) Der „Existenzsatz“ besagt, dass es zu vorgegebener, nach einem Modul 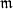 definierten Klassengruppe H von k eine abelsche Erweiterung K|k als
Klassenkörper gibt. Artin verbindet ihn mit dem „Isomorphiesatz“ (nämlich
dass A/H isomorph zur Galoisgruppe von K|k ist) und dem „speziellen
Zerlegungssatz“ (nämlich dass die Primideale aus H und nur diese in K
voll zerfallen). Im Grunde, sagt Artin, geht alles wie im „Bericht“, nur
dass manche Schlüsse einfacher werden infolge eines sorgfältig angelegten
Induktionsbeweises.
definierten Klassengruppe H von k eine abelsche Erweiterung K|k als
Klassenkörper gibt. Artin verbindet ihn mit dem „Isomorphiesatz“ (nämlich
dass A/H isomorph zur Galoisgruppe von K|k ist) und dem „speziellen
Zerlegungssatz“ (nämlich dass die Primideale aus H und nur diese in K
voll zerfallen). Im Grunde, sagt Artin, geht alles wie im „Bericht“, nur
dass manche Schlüsse einfacher werden infolge eines sorgfältig angelegten
Induktionsbeweises.
Übrigens ist der Existenzsatz in den Artinschen Göttinger Vorträgen120 nicht behandelt worden. Wahrscheinlich hat die zur Verfügung stehende Zeit nicht ausgereicht. Daraus, dass Artin den Existenzsatz aus dem Programm seiner Göttinger Vorträge gestrichen hat, können wir vielleicht entnehmen, dass er den neuen Beweis nicht zu den „ungeheuren Vereinfachungen“ zählte, von denen er in seinem Brief an Hasse spricht.