-Formulierung ist, wie ich schon immer geglaubt habe. Sie pflichten doch jetzt
bei?38
Darf ich nun einige Fragen und Bemerkungen machen:
Lieber Herr Hasse!
Vielen Dank für den wirklich wundervollen Beweis von
Furtwängler.37
Er beweist mir aufs neue, dass die „wahre“ Formulierung der Rez[iprozitäts]gesetze
die -Formulierung ist, wie ich schon immer geglaubt habe. Sie pflichten doch jetzt
bei?38
Darf ich nun einige Fragen und Bemerkungen machen:
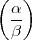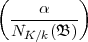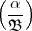k =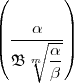 
k = 
K =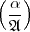 
K = 
K =
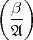K etc. an dieser Stelle nicht streng so lauten: Sei 
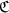ein Ideal
derselben Idealklasse in K wie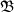 
, also ~ ~
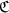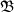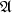. Dann ist, wenn
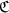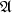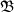prim zu und ist: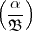
= 
= 
= 
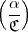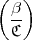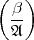, denn zum Beispiel ist 
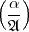gar nicht
definiert, da ja 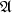ein Teiler von 
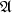ist ( = n).39
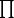
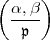= 1 beweisen wollen.40
Ich kenne mich mit den Normenrestsymbolen doch bei weitem nicht so
gut aus wie Sie, so dass Sie die Sache mit viel weniger Mühe schaffen
können wie ich. Ich bin überzeugt, dass man bei genügender Ausnützung
des „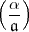
-Satzes“ die verlangte Gleichung nicht allzu schwer wird
beweisen können. Die Hauptschwierigkeit liegt doch wohl in dem Satz:
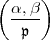ist Normenrestsymbol, d.h. 
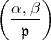= +1 dann und nur dann
wenn Normenrest nach jeder Potenz von 
in k(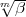
) ist. Oder ist
das leicht zu sehen? Ich bin auf Ihren Beweis sehr gespannt.
» 0 wenn m = 2 ist. Denn für m > 2 ist
k (da er die E[inheits]w[urzeln] enthält) total imaginär. Man könnte
ebensogut sagen: … und » 0.41
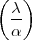= 1, wenn hyperprimär ist,
der ja aus dem „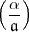
-Satz“ unmittelbar folgt.43
Alles andere könnte Ihren Publikationen vorbehalten bleiben. Ich glaube,
kleine Wiederholungen würden nicht nur nichts schaden, sondern sogar
sehr gut sein.44
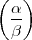
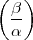-1 in beliebigen
Körpern und insbesondere im Kreiskörper für beliebiges m? Eventuell
natürlich mit Modifikationen. Sie haben doch sicher schon darüber
nachgedacht.45
-Formulierung des R[eziprozitäts]g[esetzes]
gilt in beliebigen Körpern auch ohne irgend eine Einh[eits]wurzel. Ist es
nun auch möglich, in beliebigen Körpern eine Art Normenrestsymbol
zu definieren? Ich meine das so: k sei der Körper, k' = k(
). Es sei nun
'eine Zahl aus k'46
von der Art, dass k'(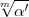
) einen cykl[ischen] Körper k0 m-ten Grades
über k enthält. Gesucht wird ein Symbol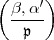 
, wo 
Zahl aus
k,' Zahl aus k' dieses Typus ist, derart, dass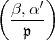 
= 1, wenn
in k0 Normenrest mod 
ist, und derart dass
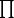
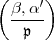= 1 ist.
Wahrscheinlich wird das nicht gehen. Aber warum nicht?47
Einerseits tut es mir leid, dass Sie nun den ganzen Bericht wiederholen müssen.48 Ich glaube aber, dass die Arbeit sich lohnen wird, da man doch die ganzen Dinge wie Eisenstein’sches Reziprozitätsgesetz ect. nicht mehr braucht und der gewonnene Platz einer genaueren Durchführung zu Gute kommen kann, die doch sehr wünschenswert wäre. Sie werden doch im zweiten Teil alle Beweise bringen?
Verzeihen Sie eine indiskrete Frage. Hecke sagte mir, dass Bessel-Hagen sich nach Halle umhabilitieren wird oder hat und dass er einen Bericht der Klassenkörpertheorie für die Annalen machen wird. Bitte ganz sachlich: Halten Sie das für gut? Würde es nicht mehr im Interesse des Gegenstandes liegen wenn Sie die Sache übernehmen? Darf ich Sie bitten dies rein sachlich und in keiner Weise persönlich zu betrachten. Diese schwierige Theorie verlangt doch einen gereiften, mit den Problemen durch eigene Arbeit vertrauten Menschen.49
Über den Hauptidealsatz später.50
Mit vielen Grüssen und einer Empfehlung an Frau Gemahlin
Ihr Artin Kommentare zum Brief Nr.10:
