10.3 Das Hilbertsche Symbol
Im Brief Nr.8 hatte Artin bereits erwähnt, dass man jetzt noch die
Hilbertsche Fassung des Reziprozitätsgesetzes gewinnen müsse, und am Ende von
Nr.9 fragt er an, ob Hasse die Produktformel für das Hilbertsche Symbol
beweisen könne.
Hilbert hatte seine Produktformel stets als den eigentlichen Kern des
Reziprozitätsgesetzes angesehen. Implizite steckte sie ja schon in Gauss’ Theorie
der Geschlechtercharaktere, mit deren Hilfe Gauss dann das Reziprozitätsgesetz
bewiesen hat. Für Hilbert stellt die Produktformel, welche, wie Hilbert sagt,
„das Reziprozitätsgesetz auf die einfachste und vollständigste Weise zum
Ausdruck bringt“, das eigentliche Analogon des Cauchyschen Satzes dar,
wonach das komplexe Integral entlang einer geschlossenen Kurve um alle
Singularitäten einer analytischen Funktion in der komplexen Ebene (oder auf
einer Riemannschen Fläche) immer gleich Null ist. Es war ja eine Forderung von
Hilbert, dass zu den wichtigen Sätzen der Funktionentheorie die analogen
Sätze in der Zahlentheorie aufzustellen seien, und in seinem Entwurf einer
allgemeinen Theorie des Klassenkörpers hat er sich auch von dieser Idee leiten
lassen.
Hasse hatte sich unter diesem Gesichtspunkt schon früher in einer Reihe von Arbeiten
mit dem Hilbertschen Symbol beschäftigt, damals für den Fall eines Primzahlexponenten
m =  .
Dies war Artin natürlich bekannt und so schreibt er jetzt in Punkt 2.) seines
Briefes, dass er sich mit den Normenrestsymbolen bei weitem nicht so gut
auskenne wie Hasse und deshalb dankbar wäre, wenn die Produktformel für das
Hilbertsche Symbol von Hasse übernommen würde. Das geschieht nun im 2.Teil
der Hasseschen Arbeit [Has27e].
.
Dies war Artin natürlich bekannt und so schreibt er jetzt in Punkt 2.) seines
Briefes, dass er sich mit den Normenrestsymbolen bei weitem nicht so gut
auskenne wie Hasse und deshalb dankbar wäre, wenn die Produktformel für das
Hilbertsche Symbol von Hasse übernommen würde. Das geschieht nun im 2.Teil
der Hasseschen Arbeit [Has27e].
Jetzt ist die Situation anders als in Hasses früheren Arbeiten bei
Primzahlexponenten. Damals war die Gültigkeit der Produktformel durch die
Arbeiten von Furtwängler und Takagi bereits gesichert und es ging darum, das
Hilbertsche Symbol 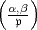 durch lokale Eigenschaften zu charakterisieren. Jetzt,
bei beliebigem Exponenten, kommt es zunächst darauf an, das Hilbertsche
Normsymbol geeignet zu definieren und die Produktformel mit Hilfe des
Artinschen Reziprozitätsgesetzes zu beweisen. Wie Artin in seinem Brief
vorhersagt, liegt die Hauptschwierigkeit darin, dass das zu definierende Symbol
wirklich die Normeigenschaft besitzt.
durch lokale Eigenschaften zu charakterisieren. Jetzt,
bei beliebigem Exponenten, kommt es zunächst darauf an, das Hilbertsche
Normsymbol geeignet zu definieren und die Produktformel mit Hilfe des
Artinschen Reziprozitätsgesetzes zu beweisen. Wie Artin in seinem Brief
vorhersagt, liegt die Hauptschwierigkeit darin, dass das zu definierende Symbol
wirklich die Normeigenschaft besitzt.
Eigentlich, so meint Hasse in [Has27e], sollte es möglich sein, das
lokale Symbol allein durch seine formalen Eigenschaften eindeutig zu
definieren, nämlich: Es bedeute k die
die  -adische Komplettierung des Körpers
k, von dem vorausgesetzt wird, dass er die m-ten Einheitswurzeln
enthält.
Dann ist (
-adische Komplettierung des Körpers
k, von dem vorausgesetzt wird, dass er die m-ten Einheitswurzeln
enthält.
Dann ist (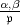 ) ein bi-multiplikatives, anti-symmetrisches Symbol auf k
) ein bi-multiplikatives, anti-symmetrisches Symbol auf k × mit
Werten in der Gruppe der m-ten Einheitswurzeln, derart dass:
× mit
Werten in der Gruppe der m-ten Einheitswurzeln, derart dass:
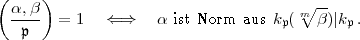 | (23) |
Aber diese formalen Eigenschaften reichen zur Definition nicht aus. Daher folgt
Hasse der Methode, welche im Falle m =  benutzt wurde, wobei nunmehr das
Artinsche Reziprozitätsgesetz herangezogen werden muss.
benutzt wurde, wobei nunmehr das
Artinsche Reziprozitätsgesetz herangezogen werden muss.
Für die nicht in m aufgehenden Primstellen  wird
wird 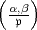 nach dem Muster
von Formel (5) auf Seite 59 definiert.
nach dem Muster
von Formel (5) auf Seite 59 definiert.
Für die Teiler  von m geht Hasse folgendermaßen vor: Gegeben seien
von m geht Hasse folgendermaßen vor: Gegeben seien
 ,
,
 k. Man wähle
k. Man wähle  ',
', '
' k im
k im  -adischen Sinne hinreichend nahe bei
-adischen Sinne hinreichend nahe bei
 ,
, ,
aber für jeden Teiler
,
aber für jeden Teiler  '≠
'≠ von m im
von m im  '-adischen Sinne hinreichend nahe bei 1.
Wenn überhaupt das Hilbertsche Symbol sinnvoll definiert werden kann, dann
sollte es stetig sein, und also
'-adischen Sinne hinreichend nahe bei 1.
Wenn überhaupt das Hilbertsche Symbol sinnvoll definiert werden kann, dann
sollte es stetig sein, und also
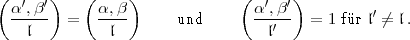
Außerdem sollte die Produktformel für  ',
', ' gelten, und das ergibt
dann:
' gelten, und das ergibt
dann:
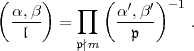 | (24) |
Hasse nimmt nun die Gleichung (24) als Definition der linken Seite. Als erstes
muss dazu gezeigt werden, dass dadurch 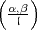 wohldefiniert ist. Dazu wird das
allgemeine Reziprozitätsgesetz (19) für das Jacobische Symbol benötigt. Die
Produktformel für das Hilbertsche Symbol ist im Grunde in die Definition (24)
eingebaut. Die funktoriellen Eigenschaften des Hilbertschen Symbols ergeben
sich routinemäßig. Einen erheblichen Aufwand erfordert der Beweis der
Normeigenschaft dieses Symbols, so wie Artin das in seinem Brief vorhergesagt
hatte. Allerdings ist der Beweis ziemlich direkt, es treten keine besonderen
Schwierigkeiten auf.
wohldefiniert ist. Dazu wird das
allgemeine Reziprozitätsgesetz (19) für das Jacobische Symbol benötigt. Die
Produktformel für das Hilbertsche Symbol ist im Grunde in die Definition (24)
eingebaut. Die funktoriellen Eigenschaften des Hilbertschen Symbols ergeben
sich routinemäßig. Einen erheblichen Aufwand erfordert der Beweis der
Normeigenschaft dieses Symbols, so wie Artin das in seinem Brief vorhergesagt
hatte. Allerdings ist der Beweis ziemlich direkt, es treten keine besonderen
Schwierigkeiten auf.
BEMERKUNG: Wie die obige Diskussion zeigt, ist die Produktformel für das
Hilbertsche Symbol im wesentlichen nur eine Umformung des allgemeinen
Reziprozitätsgesetzes (19). Sachlich bringt die Produktformel keine neue
Information, weil ja das Hilbertsche Symbol 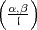 für einen kritischen
Primdivisor
für einen kritischen
Primdivisor  |m nicht unabhängig von den Primdivisoren
|m nicht unabhängig von den Primdivisoren 
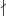 m definiert wird.
Die Situation bei beliebigem Exponenten m ist also dieselbe wie sie im Falle von
Primzahlexponenten durch Takagi beschrieben wurde. Bei der Produktformel für
das Hilbertsche Symbol, so schreibt Takagi,
m definiert wird.
Die Situation bei beliebigem Exponenten m ist also dieselbe wie sie im Falle von
Primzahlexponenten durch Takagi beschrieben wurde. Bei der Produktformel für
das Hilbertsche Symbol, so schreibt Takagi,
handelt es sich um eine Betrachtung mehr formaler Natur, und
der Beweis erledigt sich schnell durch Heranziehung des vorher
erhaltenen Resultats …
wobei das „vorher erhaltene Resultat“ eben das allgemeine Reziprozitätsgesetz ist.
Vielleicht hat Artin das auch so gesehen, als er im Brief Nr.8 meinte, dass die
Herleitung der Hilbertschen Fassung „nur etwas langweilig“ sei.
Immerhin ist zu sagen, dass Hasse die Ideen, die zur Hilbertschen
Produktformel führen, später weiter entwickelt hat und dadurch zu seinem
Normsymbol und zur Entdeckung der lokalen Klassenkörpertheorie gelangte
(siehe 26.1). Und schließlich, angeregt durch Emmy Noether, zu einer
rein lokalen Definition des Normsymbols [Has33a], und von daher mit
Hilfe des Lokal-Global-Prinzips zu einem neuen Beweis des Artinschen
Reziprozitätsgesetzes. Also doch nicht so langweilig. Wenn Artin schreibt: „Ich
bin auf Ihren Beweis sehr gespannt“, dann ist er durch diese Entwicklung, die
allerdings etwas länger dauerte, sicher nicht enttäuscht worden.
 . 59
Dies war Artin natürlich bekannt und so schreibt er jetzt in Punkt 2.) seines
Briefes, dass er sich mit den Normenrestsymbolen bei weitem nicht so gut
auskenne wie Hasse und deshalb dankbar wäre, wenn die Produktformel für das
Hilbertsche Symbol von Hasse übernommen würde. Das geschieht nun im 2.Teil
der Hasseschen Arbeit [Has27e].
. 59
Dies war Artin natürlich bekannt und so schreibt er jetzt in Punkt 2.) seines
Briefes, dass er sich mit den Normenrestsymbolen bei weitem nicht so gut
auskenne wie Hasse und deshalb dankbar wäre, wenn die Produktformel für das
Hilbertsche Symbol von Hasse übernommen würde. Das geschieht nun im 2.Teil
der Hasseschen Arbeit [Has27e].
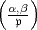 durch lokale Eigenschaften zu charakterisieren. Jetzt,
bei beliebigem Exponenten, kommt es zunächst darauf an, das Hilbertsche
Normsymbol
durch lokale Eigenschaften zu charakterisieren. Jetzt,
bei beliebigem Exponenten, kommt es zunächst darauf an, das Hilbertsche
Normsymbol

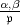
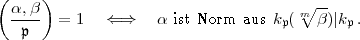
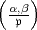 nach dem Muster
von Formel (
nach dem Muster
von Formel (
 ,
,

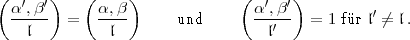
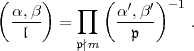
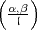 wohldefiniert ist. Dazu wird das
allgemeine Reziprozitätsgesetz
wohldefiniert ist. Dazu wird das
allgemeine Reziprozitätsgesetz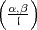 für einen kritischen
Primdivisor
für einen kritischen
Primdivisor