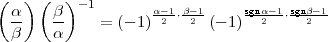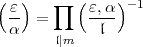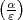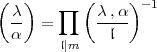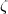4 Reziprozität für Potenzreste
Wir beabsichtigen hier nicht, auf die lange Geschichte der Reziprozitätsgesetze
einzugehen; dazu sei auf die zahlreiche einschlägige Literatur verwiesen, z.Bsp.
[Lem00] sowie [Fre94]. Unser Ziel ist es, die wichtigsten Resultate zu nennen, auf
denen Artin und Hasse aufbauten, und zwar in der Terminologie, wie sie zu
Beginn des 20.Jahrhunderts gebräuchlich war und auch von Artin in den Briefen
benutzt wurde.
Heute kennen wir das Artinsche Reziprozitätsgesetz als eine
Isomorphieaussage zwischen der Galoisgruppe einer abelschen Zahlkörpererweiterung
K|k und der zugehörigen Strahlklassengruppe (oder Idelklassengruppe) in k.
Dieser Isomorphiesatz wurde 1923 von Artin formuliert [Art23b] und 1927
bewiesen [Art27a]. Damals erschien dieser Satz, den Artin sofort als „allgemeines
Reziprozitätsgesetz“ bezeichnete, vielen Mathematikern zunächst „etwas
fremdartig“, wie Artin in seiner Arbeit selbst sagte. Vorher verstand man nämlich
unter einem „Reziprozitätsgesetz“ eine Aussage über Potenzreste, und zwar in
solchen Zahlkörpern, welche die einschlägigen Einheitswurzeln enthalten. Wir
wollen das nun erläutern.
Es sei m > 1 eine vorgegebene natürliche Zahl und k ein algebraischer
Zahlkörper, der die m-ten Einheitswurzeln enthält. Es sei  ein Primdivisor von
k und |
ein Primdivisor von
k und | | die Anzahl der Elemente seines Restklassenkörpers, also die
Absolutnorm von
| die Anzahl der Elemente seines Restklassenkörpers, also die
Absolutnorm von  . Es wird vorausgesetzt, dass
. Es wird vorausgesetzt, dass  nicht in m aufgeht. Ist
nicht in m aufgeht. Ist

 k prim zu
k prim zu  , so ist das m-te Potenzrestsymbol
, so ist das m-te Potenzrestsymbol 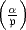 definiert als
diejenige eindeutig bestimmte m-te Einheitswurzel, welche der Kongruenz
genügt:
definiert als
diejenige eindeutig bestimmte m-te Einheitswurzel, welche der Kongruenz
genügt:
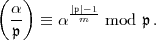 | (1) |
Wenn hervorgehoben werden soll, auf welchen Exponenten m sich das Symbol
bezieht, dann schreibt man auch 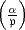 m oder
m oder 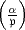 (m).
(m).
Genau dann ist 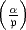 = 1, wenn
= 1, wenn  ein m-ter Potenzrest modulo
ein m-ter Potenzrest modulo  ist, d.h.
wenn die Kongruenz xm
ist, d.h.
wenn die Kongruenz xm 
 mod
mod  durch x
durch x  k lösbar ist. Wenn das der Fall ist,
so gibt es genau m solche Lösungen modulo
k lösbar ist. Wenn das der Fall ist,
so gibt es genau m solche Lösungen modulo  .
.
Für Divisoren  von k, die zu
von k, die zu  und zu m prim sind, wird
und zu m prim sind, wird 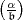 erklärt
vermöge Multiplikativität bezüglich des Nenners
erklärt
vermöge Multiplikativität bezüglich des Nenners 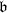 . Wenn
. Wenn 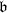 = (
= (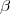 ) ein
Hauptdivisor ist, so schreibt man
) ein
Hauptdivisor ist, so schreibt man 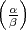 . Dies ist das Jacobische Symbol zum
Exponenten m.
. Dies ist das Jacobische Symbol zum
Exponenten m.
Als Allgemeines Reziprozitätsgesetz für das Jacobische Symbol zum
Exponenten m wird meist die folgende Aussage bezeichnet:
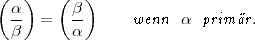 | (2) |
Vorausgesetzt wird natürlich, dass beide Symbole, auf der linken und auf der
rechten Seite, auf die angegebene Weise definiert sind, d.h.  ,
,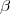 sollen zueinander
und zu m prim sein. Ferner heißt
sollen zueinander
und zu m prim sein. Ferner heißt  primär, wenn die Diskriminante von
k(
primär, wenn die Diskriminante von
k(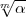 )|k prim ist zu m. Das bedeutet, dass jede in m aufgehende Primstelle
unverzweigt ist in k(
)|k prim ist zu m. Das bedeutet, dass jede in m aufgehende Primstelle
unverzweigt ist in k(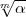 ). (Für m = 2 ist noch die Zusatzbedingung zu
stellen, dass
). (Für m = 2 ist noch die Zusatzbedingung zu
stellen, dass  total positiv ist in k, d.h. jede unendliche Stelle von k
soll in k(
total positiv ist in k, d.h. jede unendliche Stelle von k
soll in k(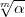 ) unverzweigt sein.) Wenn der Exponent m hervorgehoben
werden soll, so sagt man „
) unverzweigt sein.) Wenn der Exponent m hervorgehoben
werden soll, so sagt man „ ist m-primär“. Wenn m =
ist m-primär“. Wenn m = 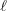 eine Primzahl
ist, dann lassen sich die primären
eine Primzahl
ist, dann lassen sich die primären  durch Kongruenzbedingungen nach
Potenzen der in
durch Kongruenzbedingungen nach
Potenzen der in 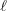 aufgehenden Primstellen
aufgehenden Primstellen  von k charakterisieren. Für
eine höhere Primzahlpotenz m =
von k charakterisieren. Für
eine höhere Primzahlpotenz m = 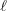 n ist eine solche Charakterisierung
schwieriger; in den Briefen Artin–Hasse kommt dieses Problem öfters zur
Sprache.
n ist eine solche Charakterisierung
schwieriger; in den Briefen Artin–Hasse kommt dieses Problem öfters zur
Sprache.
Gelegentlich wird auch der Begriff  hyperprimär benutzt; er bedeutet, dass
jede in m aufgehende Primstelle voll zerlegt ist in k(
hyperprimär benutzt; er bedeutet, dass
jede in m aufgehende Primstelle voll zerlegt ist in k(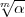 ).
).
Wenn k = 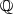 und m = 2 ist, dann handelt es in (2) sich um das gewöhnliche
quadratische Reziprozitätsgesetz; die Bedingung „
und m = 2 ist, dann handelt es in (2) sich um das gewöhnliche
quadratische Reziprozitätsgesetz; die Bedingung „ primär“ bedeutet in diesem
Falle, dass
primär“ bedeutet in diesem
Falle, dass 
 1 mod 4 und
1 mod 4 und  > 0 ist. Für einen beliebigen algebraischen
Zahlkörper und m = 2 hatte Hilbert dieses Reziprozitätsgesetz in seinen
Arbeiten behandelt. In seiner Pariser Ansprache 1900 hatte er dann das
Problem gestellt, dies für einen beliebigen Exponenten m zu verallgemeinern.
Vermöge der Primzerlegung von m kann das Problem auf den Fall einer
Primzahlpotenz m =
> 0 ist. Für einen beliebigen algebraischen
Zahlkörper und m = 2 hatte Hilbert dieses Reziprozitätsgesetz in seinen
Arbeiten behandelt. In seiner Pariser Ansprache 1900 hatte er dann das
Problem gestellt, dies für einen beliebigen Exponenten m zu verallgemeinern.
Vermöge der Primzerlegung von m kann das Problem auf den Fall einer
Primzahlpotenz m = 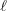 n zurückgeführt werden. Das 9.Hilbertsche Problem
lautete:
n zurückgeführt werden. Das 9.Hilbertsche Problem
lautete:
Für einen ungeraden Primzahlexponenten m = 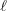 wurde das Hilbertsche
Problem in den Jahren bis 1913 durch Furtwängler erledigt. Takagi hat in
seiner 1922 erschienenen Arbeit das Reziprozitätsgesetz in den Rahmen
der Klassenkörpertheorie gestellt, so wie das Hilbert vorausgesehen
hatte.
Der Zusammenhang mit der Klassenkörpertheorie ergibt sich aus dem Bau der
Formel (1). Der Wert von
wurde das Hilbertsche
Problem in den Jahren bis 1913 durch Furtwängler erledigt. Takagi hat in
seiner 1922 erschienenen Arbeit das Reziprozitätsgesetz in den Rahmen
der Klassenkörpertheorie gestellt, so wie das Hilbert vorausgesehen
hatte.
Der Zusammenhang mit der Klassenkörpertheorie ergibt sich aus dem Bau der
Formel (1). Der Wert von 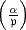 bestimmt nämlich den Zerlegungstypus der
Primstelle
bestimmt nämlich den Zerlegungstypus der
Primstelle  in der abelschen Körpererweiterung k(
in der abelschen Körpererweiterung k(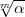 ); wenn z.Bsp.
); wenn z.Bsp.
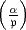 = 1 so zerfällt
= 1 so zerfällt  voll. Ganz allgemein war nun aber die Beschreibung
des Zerlegungstypus von Primstellen in abelschen Erweiterungen das
Hauptproblem, aus dem sich die Klassenkörpertheorie entwickelt hatte –
unabhängig von Voraussetzungen über Einheitswurzeln im Grundkörper. (Vgl.
[Fre89].)
voll. Ganz allgemein war nun aber die Beschreibung
des Zerlegungstypus von Primstellen in abelschen Erweiterungen das
Hauptproblem, aus dem sich die Klassenkörpertheorie entwickelt hatte –
unabhängig von Voraussetzungen über Einheitswurzeln im Grundkörper. (Vgl.
[Fre89].)
Durch seinen klassenkörpertheoretischen Ansatz erhielt Takagi ebenfalls eine
Lösung des Hilbertschen 9.Problems für Primzahlexponenten, aber auf anderem
Weg als Furtwängler. Der Fall eines beliebigen Primzahlpotenz-Exponenten
m = 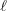 n konnte jedoch erst durch Artin auf der Basis seines Reziprozitätsgesetzes
erledigt werden, unter Verwendung von Ideen von Hasse und Furtwängler. Davon
zeugen die späteren Briefe aus dem Jahr 1927.
n konnte jedoch erst durch Artin auf der Basis seines Reziprozitätsgesetzes
erledigt werden, unter Verwendung von Ideen von Hasse und Furtwängler. Davon
zeugen die späteren Briefe aus dem Jahr 1927.
In Verallgemeinerung des allgemeinen Reziprozitätsgesetzes (2) entsteht die
Frage nach der Berechnung des sogenannten Umkehrfaktors:
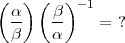 | (3) |
in denjenigen Fällen, in denen die obige Bedingung des Reziprozitätsgesetzes
nicht erfüllt ist, in denen also weder  noch
noch 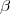 primär ist. Zur Präzisierung dieser
Aufgabe hat Hilbert das nach ihm benannte Hilbertsche Normsymbol
primär ist. Zur Präzisierung dieser
Aufgabe hat Hilbert das nach ihm benannte Hilbertsche Normsymbol 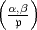 eingeführt, das in gewissem Sinne schon bei Eisenstein (1850) vorkommt und im
wesentlichen auf Gauss (1801) zurückgeht, wo es „Charakter“ genannt wird. Es
besitzt die folgenden Eigenschaften:
eingeführt, das in gewissem Sinne schon bei Eisenstein (1850) vorkommt und im
wesentlichen auf Gauss (1801) zurückgeht, wo es „Charakter“ genannt wird. Es
besitzt die folgenden Eigenschaften:
Für jede Primstelle  von k ist
von k ist 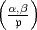 eine bimultiplikative
antisymmetrische Funktion in
eine bimultiplikative
antisymmetrische Funktion in  und
und 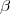 mit Werten aus der Gruppe der
m-ten Einheitswurzeln, und zwar derart, dass
mit Werten aus der Gruppe der
m-ten Einheitswurzeln, und zwar derart, dass 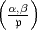 = 1 wenn und
nur wenn
= 1 wenn und
nur wenn  eine Norm aus der
eine Norm aus der  -adischen Komplettierung k
-adischen Komplettierung k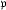 (
(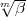 )
ist.
Dabei dürfen
)
ist.
Dabei dürfen  ,
,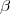 beliebige Elemente aus k (oder k
beliebige Elemente aus k (oder k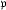 ) sein. Die Definition des
Normsymbols war keineswegs einfach, jedenfalls wenn
) sein. Die Definition des
Normsymbols war keineswegs einfach, jedenfalls wenn  ein Teiler des Exponenten
m ist, und sie benutzte insbesondere das allgemeine Reziprozitätsgesetz.
Demgemäß konnte Hilbert selbst nur den quadratischen Fall m = 2 behandeln;
der Fall eines ungeraden Primzahlexponenten m =
ein Teiler des Exponenten
m ist, und sie benutzte insbesondere das allgemeine Reziprozitätsgesetz.
Demgemäß konnte Hilbert selbst nur den quadratischen Fall m = 2 behandeln;
der Fall eines ungeraden Primzahlexponenten m = 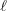 wurde erst durch
Furtwängler und Takagi erledigt. Der Fall eines beliebigen Exponenten m konnte
erst von Hasse aufgrund des Artinschen Reziprozitätsgesetzes behandelt
werden.
wurde erst durch
Furtwängler und Takagi erledigt. Der Fall eines beliebigen Exponenten m konnte
erst von Hasse aufgrund des Artinschen Reziprozitätsgesetzes behandelt
werden.
Ohne hier auf die genaue Definition einzugehen, stellen wir lediglich fest, dass
die Produktformel für das Hilbertsche Symbol gilt:
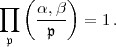 | (4) |
(Hierbei sind auch die reellen unendlichen Primstellen  zu berücksichtigen, falls
es welche gibt; das kann nur für m = 2 eintreten). In dieser Produktformel
hatte Hilbert alle Reziprozitätsbeziehungen für die m-ten Potenzreste in k
zusammengefasst.
zu berücksichtigen, falls
es welche gibt; das kann nur für m = 2 eintreten). In dieser Produktformel
hatte Hilbert alle Reziprozitätsbeziehungen für die m-ten Potenzreste in k
zusammengefasst.
Wenn  kein Teiler von m ist, so lässt sich das Hilbertsche Symbol in einfacher
Weise durch das Jacobische Symbol wie folgt ausdrücken:
kein Teiler von m ist, so lässt sich das Hilbertsche Symbol in einfacher
Weise durch das Jacobische Symbol wie folgt ausdrücken:
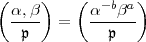 | (5) |
wobei a = v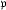 (
( ) und b = v
) und b = v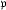 (
(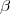 ) die Ordnungszahlen von a,b bei der zu
) die Ordnungszahlen von a,b bei der zu  gehörigen Exponentenbewertung v
gehörigen Exponentenbewertung v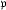 von k bezeichnen. (Wenn m gerade und nicht
durch 4 teilbar ist, dann ist auf der rechten Seite noch der Faktor
von k bezeichnen. (Wenn m gerade und nicht
durch 4 teilbar ist, dann ist auf der rechten Seite noch der Faktor 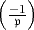 ab
hinzuzufügen.) Wenn
ab
hinzuzufügen.) Wenn  ,
,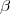 zueinander und zu m prim sind, wie es in (3)
vorausgesetzt ist, dann ersieht man aus (5), dass
zueinander und zu m prim sind, wie es in (3)
vorausgesetzt ist, dann ersieht man aus (5), dass 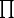
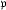
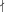 m
m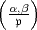 =
= 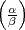
 -1.
Zufolge der Produktformel (4) lässt sich also der Umkehrfaktor wie folgt
darstellen:
-1.
Zufolge der Produktformel (4) lässt sich also der Umkehrfaktor wie folgt
darstellen:
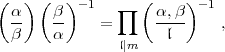 | (6) |
(wobei auf der rechten Seite auch die reellen Primstellen von k zu berücksichtigen
sind, was nur für m = 2 relevant ist). Oft wird auch diese Formel für den
Umkehrfaktor als „allgemeines Reziprozitätsgesetz“ bezeichnet; sie enthält (2) als
Spezialfall.
Durch (6) ist zwar die Aufgabe (3) nicht gelöst, weil die (Hilbertsche)
Definition der Normsymbole 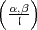 für
für  ∣m formaler Natur ist und keinen
expliziten Aufschluss über den Wert dieser Symbole liefert. Durch (6) wird aber
die Aufgabe für den Umkehrfaktor zurückgeführt auf die Berechnung der
Hilbertschen Normsymbole an denjenigen Primstellen
∣m formaler Natur ist und keinen
expliziten Aufschluss über den Wert dieser Symbole liefert. Durch (6) wird aber
die Aufgabe für den Umkehrfaktor zurückgeführt auf die Berechnung der
Hilbertschen Normsymbole an denjenigen Primstellen  in k, die Teiler von m sind
(und die unendlichen reellen Primstellen für m = 2). Das führt auf die
sogenannten expliziten Reziprozitätsformeln.
in k, die Teiler von m sind
(und die unendlichen reellen Primstellen für m = 2). Das führt auf die
sogenannten expliziten Reziprozitätsformeln.
Im Spezialfall k = 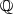 und m = 2 sind diese expliziten Formeln nach dem
quadratischen Reziprozitätsgesetz in der Form geläufig:
und m = 2 sind diese expliziten Formeln nach dem
quadratischen Reziprozitätsgesetz in der Form geläufig:
Auf der rechten Seite entspricht der erste Faktor der Primstelle 2, während der
zweite Faktor zur reellen Stelle von 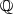 gehört. (Dieser fällt weg, wenn
gehört. (Dieser fällt weg, wenn
 > 0 oder
> 0 oder 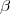 > 0 ist.) In den Jahren 1923-25 hat Hasse versucht, explizite
Reziprozitätsformeln mit möglichst großem Gültigkeitsbereich zu finden, und
zwar zunächst im Falle eines Primzahlexponenten m =
> 0 ist.) In den Jahren 1923-25 hat Hasse versucht, explizite
Reziprozitätsformeln mit möglichst großem Gültigkeitsbereich zu finden, und
zwar zunächst im Falle eines Primzahlexponenten m = 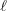 . In späteren Jahren –
nachdem Artin sein Reziprozitätsgesetz gefunden hatte – dann auch für
Primzahlpotenz-Exponenten m =
. In späteren Jahren –
nachdem Artin sein Reziprozitätsgesetz gefunden hatte – dann auch für
Primzahlpotenz-Exponenten m = 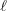 n.
n.
Wir weisen noch einmal darauf hin, dass die Produktformel (4) und
auch (6) auf dem Reziprozitätsgesetz (2) beruhen und somit vor Artin nur
im Falle eines Primzahlexponenten m = 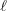 gesichert waren. Erst auf der
Grundlage des Artinschen Reziprozitätsgesetzes 1927 wurde es schließlich
möglich, diese für einen beliebigen Exponenten m zu verifizieren. Demgemäß
beziehen sich die ersten 5 Briefe aus dem Jahr 1923, als das Artinsche
Reziprozitätsgesetz noch nicht bekannt war, ausschließlich auf den Fall eines
Primzahlexponenten.
gesichert waren. Erst auf der
Grundlage des Artinschen Reziprozitätsgesetzes 1927 wurde es schließlich
möglich, diese für einen beliebigen Exponenten m zu verifizieren. Demgemäß
beziehen sich die ersten 5 Briefe aus dem Jahr 1923, als das Artinsche
Reziprozitätsgesetz noch nicht bekannt war, ausschließlich auf den Fall eines
Primzahlexponenten.
Neben dem allgemeinen Reziprozitätsgesetz (2) stehen die sogenannten
Ergänzungssätze. Traditionsgemäß unterscheidet man zwischen dem
„ersten“ und dem „zweiten“ Ergänzungssatz. Der erste Ergänzungssatz
bezieht sich auf das Potenzrestsymbol für eine Einheit  des Körpers k und
lautet:
des Körpers k und
lautet:
wenn  zu m prim ist. (Für m = 2 sind auf der rechten Seite auch die
reellen Primstellen von k zu berücksichtigen.) In dieser Form ist der erste
Ergänzungssatz ein Spezialfall von (6), weil nämlich definitionsgemäß
zu m prim ist. (Für m = 2 sind auf der rechten Seite auch die
reellen Primstellen von k zu berücksichtigen.) In dieser Form ist der erste
Ergänzungssatz ein Spezialfall von (6), weil nämlich definitionsgemäß 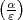 = 1
ist. Demnach ist der erste Ergänzungssatz lediglich von historischem Interesse
und spielt auch in dem Briefwechsel Artin–Hasse keine Rolle.
= 1
ist. Demnach ist der erste Ergänzungssatz lediglich von historischem Interesse
und spielt auch in dem Briefwechsel Artin–Hasse keine Rolle.
Der zweite Ergänzungssatz bezieht sich auf das Potenzrestsymbol für eine
Zahl 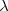
 k, die sich nur aus Primteilern des Exponenten m zusammensetzt und
lautet:
k, die sich nur aus Primteilern des Exponenten m zusammensetzt und
lautet:
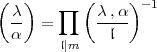 | (7) |
wenn  zu m prim ist.
zu m prim ist.
Die ersten 5 Briefe beziehen sich auf den zweiten Ergänzungssatz und sein
Verhältnis zu dem allgemeinen Reziprozitätsgesetz (2), und zwar wie bereits
gesagt im Falle eines ungeraden Primzahlexponenten 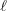 . Der dabei wohl wichtigste
Fall ist der, wenn k =
. Der dabei wohl wichtigste
Fall ist der, wenn k = 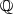 (
(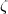 ) der Körper der
) der Körper der 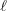 -ten Einheitswurzeln ist – unter
-ten Einheitswurzeln ist – unter 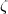 eine primitive
eine primitive 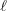 -te Einheitswurzel verstanden. In diesem Fall gibt es nur einen
einzigen Primteiler
-te Einheitswurzel verstanden. In diesem Fall gibt es nur einen
einzigen Primteiler  von k, der ein Teiler von
von k, der ein Teiler von 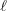 ist, und dieser besitzt 1 -
ist, und dieser besitzt 1 - 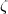 als
Primelement. Also gibt es auf der rechten Seite der Formel (7) nur einen einzigen
Faktor, und (7) braucht nur für das eine Element
als
Primelement. Also gibt es auf der rechten Seite der Formel (7) nur einen einzigen
Faktor, und (7) braucht nur für das eine Element 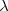 = 1 -
= 1 - 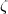 ausgewertet zu
werden.
ausgewertet zu
werden.
Schließlich ist noch das sogenannte Eisensteinsche Reziprozitätsgesetz zu
erwähnen, das in dem Briefwechsel gelegentlich erwähnt wird. Es bezieht sich
zunächst auf einen ungeraden Primzahlexponenten m = 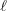 und den Körper
k =
und den Körper
k = 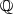 (
(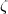 ) der
) der 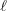 -ten Einheitswurzeln. Es handelt sich um eine gewisse Vorstufe des
Reziprozitätsgesetzes (2), nämlich unter der einschränkenden Annahme, dass
-ten Einheitswurzeln. Es handelt sich um eine gewisse Vorstufe des
Reziprozitätsgesetzes (2), nämlich unter der einschränkenden Annahme, dass  rational ist und
rational ist und 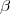 zu einer rationalen Zahl modulo
zu einer rationalen Zahl modulo  2 kongruent ist. (Dabei ist
2 kongruent ist. (Dabei ist  der Primteiler von
der Primteiler von 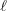 in
in 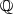 (
(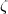 ).) Hilbert bemerkt dazu in seinem Zahlbericht, dass
das
).) Hilbert bemerkt dazu in seinem Zahlbericht, dass
das
„Eisensteinsche Reziprozitätsgesetz ein bisher unentbehrliches
Hilfsmittel zum Beweis des allgemeinen Reziprozitätsgesetzes“
ist. Takagi sagt dasselbe in seiner großen, dem Reziprozitätsgesetz gewidmeten
Arbeit 1922. Bevor Artins Reziprozitätsgesetz etabliert war, hatte man versucht,
das Eisensteinsche Reziprozitätsgesetz zu verallgemeinern auf beliebige
Primzahlpotenzexponenten m = 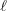 n, weil man hoffte, auf diese Weise einen
Zugang zu dem allgemeinen Reziprozitätsgesetz zu erhalten. Siehe dazu Teil II,
Abschnitt 6.3. Durch den Artinschen Beweis des Reziprozitätsgesetzes verlor
jedoch das Eisensteinsche Reziprozitätsgesetz seine Rolle als „unentbehrliches
Hilfsmittel zum Beweis des allgemeinen Reziprozitätsgesetzes“, d.h. es wurde für
diesen Zweck entbehrlich.
n, weil man hoffte, auf diese Weise einen
Zugang zu dem allgemeinen Reziprozitätsgesetz zu erhalten. Siehe dazu Teil II,
Abschnitt 6.3. Durch den Artinschen Beweis des Reziprozitätsgesetzes verlor
jedoch das Eisensteinsche Reziprozitätsgesetz seine Rolle als „unentbehrliches
Hilfsmittel zum Beweis des allgemeinen Reziprozitätsgesetzes“, d.h. es wurde für
diesen Zweck entbehrlich.
 ein Primdivisor von
k und |
ein Primdivisor von
k und | | die Anzahl der Elemente seines Restklassenkörpers, also die
Absolutnorm von
| die Anzahl der Elemente seines Restklassenkörpers, also die
Absolutnorm von  . Es wird vorausgesetzt, dass
. Es wird vorausgesetzt, dass  nicht in m aufgeht. Ist
nicht in m aufgeht. Ist

 k prim zu
k prim zu  , so ist das m-te Potenzrestsymbol
, so ist das m-te Potenzrestsymbol 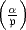 definiert als
diejenige eindeutig bestimmte m-te Einheitswurzel, welche der Kongruenz
genügt:
definiert als
diejenige eindeutig bestimmte m-te Einheitswurzel, welche der Kongruenz
genügt:
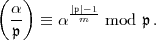
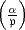
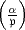
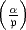

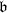
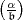 erklärt
vermöge Multiplikativität bezüglich des Nenners
erklärt
vermöge Multiplikativität bezüglich des Nenners 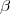
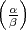 . Dies ist das
. Dies ist das 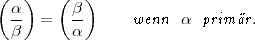

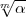
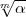
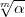
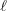

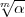
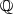
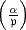 bestimmt nämlich den
bestimmt nämlich den 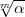
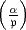
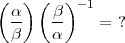
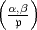 eingeführt, das in gewissem Sinne schon bei Eisenstein (1850) vorkommt und im
wesentlichen auf Gauss (1801) zurückgeht, wo es „Charakter“ genannt wird. Es
besitzt die folgenden Eigenschaften:
eingeführt, das in gewissem Sinne schon bei Eisenstein (1850) vorkommt und im
wesentlichen auf Gauss (1801) zurückgeht, wo es „Charakter“ genannt wird. Es
besitzt die folgenden Eigenschaften:
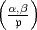 eine bimultiplikative
antisymmetrische Funktion in
eine bimultiplikative
antisymmetrische Funktion in 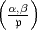
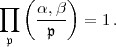
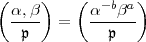
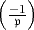
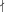
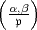
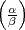

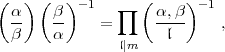
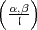 für
für