5.4 Zweiter Ergänzungssatz

Die Formel (12) ist zwar vom Typus des zweiten Ergänzungssatzes, aber sie stellt noch nicht die schärfste Form dieses Satzes dar. Denn erstens erscheint die dortige Kongruenzbedingung 1 mod zu stark; gewünscht ist eine Formel, die im „Nenner“ des Jacobischen Symbols beliebige zu prime Elemente  zulässt. Und zweitens sollte im „Zähler“ ein beliebiges Element zugelassen sein, das sich nur aus Primteilern von zusammensetzt.

In den ersten 5 Briefen Artins erleben wir die Suche nach solcherart Verallgemeinerung. Und zwar zunächst für den -ten Einheitswurzelkörper k = (). In diesem gibt es nur einen einzigen Primteiler von . Dies ist ein Hauptdivisor = (), erzeugt von dem Primelement = 1 - , und es ist ()^-1 = ().

Schon im ersten Brief wird es klar, dass Artin es nicht bei der „schönen Formel“ (12) von Hasse belassen will. Sondern er versucht, die in (12) auftretende Kongruenzbedingung 1 mod abzuschwächen, indem er nur 1 mod verlangt. Er ist so angetan von seinem Ergebnis, dass er mit Emphase ausruft: „Nun aber kommt das Schöne! “ und das Ergebnis einrahmt. Allerdings muss er bald nach Absendung des Briefes einsehen, dass in seiner Rechnung ein Fehler steckte, und er sendet noch am selben Tag eine Postkarte hinterher mit der richtigen Formel.

Aber auch diese ist noch nicht endgültig. An einem der nächsten Tage (der Brief trägt kein Datum) schickt Artin eine Formel für 1 mod 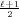statt 1 mod . Nun ist keine Rede mehr von dem Umdrehverfahren; die Rechnungen sind kunstvoll, langwierig und unübersichtlich. Es tauchen dabei Reihen auf, die als Anfänge von Logarithmen-Reihen gedeutet werden können. Artin hofft, dass diese dritte Mitteilung die letzte ist; gemeint ist natürlich die letzte vor seinem Wochenend-Besuch bei Hasse in Kiel, zu dem er am Samstag, den 14.Juli 1923 fahren will. Aber Hasse hatte offenbar sofort auf Artins Brief geantwortet, und so gibt es daraufhin doch noch eine weitere Mitteilung (wiederum ohne Datum).

Wir wissen nicht, was Hasse geschrieben hatte. Wir lesen aber in Artins Brief, dass Hasses „Herleitung selbstverständlich einfacher“ ist. Und wir bemerken, dass Artin jetzt -adische Logarithmen verwendet. Er schreibt, dass er Fortschritte in -adik macht. Daraus kann man vielleicht schließen, dass Hasse ihn auf die Vorzüge des -adischen Rechnens und insbesondere auf den -adischen Logarithmus aufmerksam gemacht hatte, der ja implizit schon in den Artinschen Rechnungen des vorangegangenen Briefes vorkam.

Die neue Formel von Artin gilt für 1 mod ². Es war ihm also gelungen, die Kongruenzbedingung noch weiter herunterzudrücken. Im Zähler des Jacobischen Symbols steht jetzt nicht sondern . Wir erinnern daran, dass ein Primelement für den einzigen Primteiler von in () ist. Also ist jede Zahl aus (), die sich nur aus Primteilern von zusammensetzt, bis auf einen Einheitsfaktor eine Potenz von , und im Prinzip lässt sich daher das Symbol 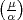mit Hilfe von 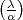berechnen.

Insbesondere gilt das für = . In einer weiteren Mitteilung, welche jetzt die Nummer VIII trägt, führt Artin dies für 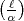im Detail aus. Vielleicht hatte ihn Hasse danach gefragt? Diesmal handelt es sich um eine Postkarte, und aus dem Poststempel können wir das Absendedatum ersehen: es war am Donnerstag, dem 12.Juli 1923, zwei Tage vor Artins Besuch bei Hasse am Samstag.

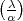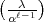Aber auch diese Ergebnisse waren noch nicht endgültig. Während Artins Besuch bei Hasse in Kiel wurden offenbar die Details noch einmal durchgesprochen und es stellte sich eine Formel heraus, die für beliebige 1 mod gilt. Diese Kongruenzbedingung ist jedoch nicht einschneidend, denn für eine beliebige, zu prime Zahl aus () gilt ^-1 1 mod und = ^-1.

Die endgültigen Formeln stehen in der gemeinsamen Arbeit [AH25]¹⁸ und lauten wie folgt. Die Situation ist dieselbe wie in (12).

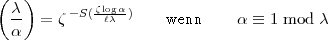(14)

und:

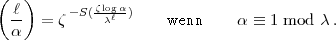(15)

Bemerkenswert an diesem Ergebnis ist, dass in diesen Formeln der -adische Logarithmus vorkommt, der für 1 mod definiert ist.

In einer Fußnote zu dieser Arbeit heißt es:

Der jüngere war Hasse.

Die Formeln (14) und (15) sind im Einheitswurzelkörper (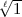) als die feinstmögliche Formulierung des zweiten Ergänzungssatzes und somit als endgültig zu betrachten. Sie gelten wörtlich auch in Oberkörpern k (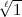), worauf in [AH25] eigens hingewiesen wird; S bedeutet dann die Spur von k nach . Die Zurückführung auf den Einheitswurzelkörper erfolgt mit der bereits im Brief Nr.1 von Artin mit Hinweis auf Takagi erwähnten funktoriellen Eigenschaft des Jacobischen Symbols, die Erweiterung des Grundkörpers betreffend.

Aber in einem solchen Oberkörper k ist (14) i.allg. nicht mehr die feinstmögliche Formulierung, weil ja in k der Primdivisor = 1 - von (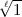) noch zerfallen kann und dann noch diejenigen Potenzrestsymbole auszudrücken bleiben, deren Zähler einen Primfaktor von nur einmal enthalten. Dieser Aufgabe hat sich Hasse in einer weiteren Arbeit [Has25b] unterzogen, die noch im selben Band des Crelleschen Journals erschienen ist. Allerdings hat Hasse dabei nur solche Körper k in den Griff bekommen, in denen der Primdivisor von () unverzweigt ist.