 n
n n
n In dem vorliegenden Brief sehen wir Artin an der Arbeit, genauer
an der Rechenarbeit. Er vermutet, anscheinend aufgrund numerischer
Evidenz, die Gültigkeit der im Brief eingerahmten Formel für das  n-te
Potenzrestsymbol.143
Es handelt sich um den 2.Ergänzungssatz. Artin arbeitet hier im Körper k =
n-te
Potenzrestsymbol.143
Es handelt sich um den 2.Ergänzungssatz. Artin arbeitet hier im Körper k =  (
(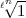 )
der
)
der  n-ten Einheitswurzeln; dort ist
n-ten Einheitswurzeln; dort ist  n ein Primelement für den (einzigen) Primteiler
n ein Primelement für den (einzigen) Primteiler
 von
von  . Artin setzt voraus, dass
. Artin setzt voraus, dass 
 1 mod
1 mod  n ; dies garantiert zwar noch nicht,
dass
n ; dies garantiert zwar noch nicht,
dass  unverzweigt ist in k(
unverzweigt ist in k(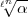 ), d.h. dass
), d.h. dass 
 n-primär ist für
n-primär ist für  . Wenn aber
. Wenn aber 
 n-primär ist, so stellt Artin fest, dass nach der „Hasseschen Formulierung des
Reziprozitätsgesetzes“ 144
gilt:
n-primär ist, so stellt Artin fest, dass nach der „Hasseschen Formulierung des
Reziprozitätsgesetzes“ 144
gilt:
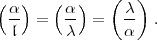
Demnach liefert dann die eingerahmte Formel dieses Briefes, im Körper der
 n-ten Einheitswurzeln, auch eine explizite Formel für das Symbol
n-ten Einheitswurzeln, auch eine explizite Formel für das Symbol 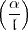 , das er
im Brief Nr.14 vom 6.8.1927 diskutiert hatte. (Dort schrieb Artin
, das er
im Brief Nr.14 vom 6.8.1927 diskutiert hatte. (Dort schrieb Artin  statt
statt  .)
Siehe 14.2.
.)
Siehe 14.2.
Für den Exponenten  erscheint die eingerahmte Formel bereits in der
gemeinsamen Arbeit von Artin und Hasse aus dem Jahre 1923. Jetzt geht es
also darum, sie für
erscheint die eingerahmte Formel bereits in der
gemeinsamen Arbeit von Artin und Hasse aus dem Jahre 1923. Jetzt geht es
also darum, sie für  2 und allgemeiner für beliebigen Exponenten
2 und allgemeiner für beliebigen Exponenten  n zu
beweisen.
n zu
beweisen.
Zwar kann Artin diese Formel nur in den von ihm angegebenen speziellen
Fällen beweisen. Er teilt Hasse alles mit, was er darüber weiß, in der Hoffnung,
dass Hasse da etwas einfällt, weil seine (Artins) rechnerische Geduld nicht
ausreicht, weil er aber andererseits fest davon überzeugt ist, dass dies der zweite
Ergänzungssatz im Kreiskörper ist. Im nächsten Brief Nr.17 vom 27.10.1927
werden wir sehen, dass Hasse in der Tat einen Beweis liefern kann. Die
Formel ist dann in die gemeinsame Arbeit von Artin und Hasse [AH28]
eingegangen. Überdies gilt die Formel nicht nur im Kreiskörper selbst,
sondern in jedem Zahlkörper k, der die  n-ten Einheitswurzeln enthält.
n-ten Einheitswurzeln enthält.