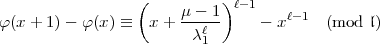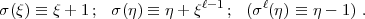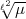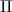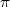14 06.08.1927, Brief von Artin an Hasse
Hamburg, am 6. August 1927
Lieber Herr Hasse!
Sie haben mir anscheinend den Ausdruck  -Ge-ixe übel vermerkt. Ich wollte
damit weiss Gott nichts gegen die
-Ge-ixe übel vermerkt. Ich wollte
damit weiss Gott nichts gegen die  -adik sagen von der ich sehr wohl weiss,
dass sie für die Behandlung der Rez[iprozitäts]ges[etze] unentbehrlich
ist. Mich ärgerte nur das
-adik sagen von der ich sehr wohl weiss,
dass sie für die Behandlung der Rez[iprozitäts]ges[etze] unentbehrlich
ist. Mich ärgerte nur das  und
und 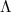 -Geixe bei Takagi an der Stelle der
Normenreste, die dort auftretenden langwierigen und doch langweiligen
Rechnungen mit Potenzsummen, das „Klettern“ auf höhere Exponenten
und all die „schönen“ Dinge. Ich glaube, da sind Sie doch auch meiner
Meinung. Dasselbe tritt dann bei den Geschlechtern nochmals auf. Was
das
-Geixe bei Takagi an der Stelle der
Normenreste, die dort auftretenden langwierigen und doch langweiligen
Rechnungen mit Potenzsummen, das „Klettern“ auf höhere Exponenten
und all die „schönen“ Dinge. Ich glaube, da sind Sie doch auch meiner
Meinung. Dasselbe tritt dann bei den Geschlechtern nochmals auf. Was
das  -Ge-ixe bei der Ranguntersuchung betrifft, so beachten Sie bitte:
Es ist nur ein „klein-
-Ge-ixe bei der Ranguntersuchung betrifft, so beachten Sie bitte:
Es ist nur ein „klein- “-Ge-ixe und nicht allzulang; bei weitem nicht so
hässlich wie bei den Normenresten. Was dann die relativen Grundeinheiten
betrifft ,
so kommt mein ganz besonderer Zorn auf sie daher, weil ich mich im
Kolleg zweimal verheddert habe und erst nach dem dritten Mal alles
einwandfrei erledigte. Mein besonderer Fluch gilt dem Symbol [
“-Ge-ixe und nicht allzulang; bei weitem nicht so
hässlich wie bei den Normenresten. Was dann die relativen Grundeinheiten
betrifft ,
so kommt mein ganz besonderer Zorn auf sie daher, weil ich mich im
Kolleg zweimal verheddert habe und erst nach dem dritten Mal alles
einwandfrei erledigte. Mein besonderer Fluch gilt dem Symbol [ ], dessen
besondere Tücken sich – natürlich – im Fall
], dessen
besondere Tücken sich – natürlich – im Fall  = 2 offenbaren. Wissen Sie
wenigstens in diesem Fall ein einfaches Hilfsmittel? Man muss da schrecklich
„klettern“.
= 2 offenbaren. Wissen Sie
wenigstens in diesem Fall ein einfaches Hilfsmittel? Man muss da schrecklich
„klettern“.
Ich habe übrigens gestern und heute andauernd  -ge-ixt.
Ohne Erfolg. Ihre Bemerkungen zu
-ge-ixt.
Ohne Erfolg. Ihre Bemerkungen zu 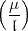 im Fall
im Fall  n hatten mich
gereizt.
Mir war natürlich klar, dass die „gewöhnliche Definition“ bei
n hatten mich
gereizt.
Mir war natürlich klar, dass die „gewöhnliche Definition“ bei  =
=  versagt, in der
Arbeit
bin ich deshalb nicht darauf eingegangen, weil dort (stillschweigend – denn bisher
handhabte man
versagt, in der
Arbeit
bin ich deshalb nicht darauf eingegangen, weil dort (stillschweigend – denn bisher
handhabte man 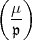 meistens so)
meistens so)  fremd zu m vorausgesetzt wurde. In meinem
ersten oder zweiten Brief an Sie habe ich aber, glaube ich, den Fall
fremd zu m vorausgesetzt wurde. In meinem
ersten oder zweiten Brief an Sie habe ich aber, glaube ich, den Fall  =
=  gestreift, hatte mir aber bis jetzt noch nicht überlegt, welche Zahl zu
nehmen ist. Ihr Resultat und vor allem die schöne Formel für
gestreift, hatte mir aber bis jetzt noch nicht überlegt, welche Zahl zu
nehmen ist. Ihr Resultat und vor allem die schöne Formel für 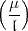 ist doch
neu? Vielleicht ist es Ihnen aber doch nützlich, wenn auch vielleicht nicht
neu, wenn ich Ihnen meine „Erfahrungen“ über
ist doch
neu? Vielleicht ist es Ihnen aber doch nützlich, wenn auch vielleicht nicht
neu, wenn ich Ihnen meine „Erfahrungen“ über 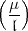 schreibe. Ich habe
nur den Fall
schreibe. Ich habe
nur den Fall  2 versucht. Denn wenn man da durchkommt, gelingt es
sicher auch allgemein. Ich schreibe wie Sie:
2 versucht. Denn wenn man da durchkommt, gelingt es
sicher auch allgemein. Ich schreibe wie Sie:  1 =
1 =  -te E[inheits]w[urzel];
-te E[inheits]w[urzel];
 1 = 1 -
1 = 1 -  1.
1.
Der von Ihnen angegebene Modul  2
2 1 für
1 für  2 primär ist es nun in dem Sinn:
Wenn
2 primär ist es nun in dem Sinn:
Wenn 
 x
x 2
(mod
2
(mod  2
2 1), so ist
1), so ist  sicher
sicher  2 primär. Sie schreiben nun, der Modul
2 primär. Sie schreiben nun, der Modul
 2
2 1 sei für
1 sei für  ≠2 auch erforderlich. Ich kann dem nur den folgenden Sinn
zuschreiben: Für keinen kleineren Modul folgt aus der angegebenen Kongruenz
dass allgemein
≠2 auch erforderlich. Ich kann dem nur den folgenden Sinn
zuschreiben: Für keinen kleineren Modul folgt aus der angegebenen Kongruenz
dass allgemein 
 2-primär ist. Ich glaube aber nicht, dass diese Kongruenz
(bez. die zugehörige für den Primteiler
2-primär ist. Ich glaube aber nicht, dass diese Kongruenz
(bez. die zugehörige für den Primteiler  – ich bleibe der Einfachheit halber bei
– ich bleibe der Einfachheit halber bei
 1) erforderlich ist.
1) erforderlich ist.
Denn wenn 
 x
x 2
(mod
2
(mod  2
2 1), so ist doch insbesondere
1), so ist doch insbesondere  sicher
sicher
 -hyperprimär.
Also zerfällt
-hyperprimär.
Also zerfällt  in k(
in k(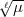 ), so dass durch diese Forderung sicher nicht der Fall erfasst
wird, wo
), so dass durch diese Forderung sicher nicht der Fall erfasst
wird, wo  in k(
in k(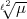 ) unzerlegt bleibt. In der Überzeugung, dass dieser Fall zuerst
untersucht werden muss, nahm ich ihn mir vor. Dann muss es eine Zahl x aus k geben,
so dass
) unzerlegt bleibt. In der Überzeugung, dass dieser Fall zuerst
untersucht werden muss, nahm ich ihn mir vor. Dann muss es eine Zahl x aus k geben,
so dass 
 x
x (mod
(mod 
 1) ist und eine Zahl y aus k(
1) ist und eine Zahl y aus k(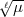 ), so dass
), so dass 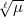
 y
y (mod
(mod 
 1)
ist.
Das x kann man natürlich zu 1 normieren. Nicht aber y; denn das ist ja dem
Körper k(
1)
ist.
Das x kann man natürlich zu 1 normieren. Nicht aber y; denn das ist ja dem
Körper k(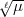 ) entnommen. Deshalb kommt man – wenigstens ich – nicht auf den
Modul
) entnommen. Deshalb kommt man – wenigstens ich – nicht auf den
Modul  2
2 1 beim heruntersteigen, ich habe das herunterklettern überhaupt
nicht fertig gebracht. Nach mehreren vergeblichen Versuchen liess ich es
liegen.
1 beim heruntersteigen, ich habe das herunterklettern überhaupt
nicht fertig gebracht. Nach mehreren vergeblichen Versuchen liess ich es
liegen.
Dann versuchte ich die „richtige Zahl“ zu finden und begann mit den ganz
schlechten Ansätzen (wie ich hinterher merkte)
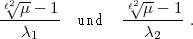 Ging alles nicht recht. Dann dachte ich etwas respektvoller darüber nach und
entdeckte, dass hier ein „alter Bekannter“ von mir vorlag. Ich dachte immer an
den „schärfsten Fall“ dass
Ging alles nicht recht. Dann dachte ich etwas respektvoller darüber nach und
entdeckte, dass hier ein „alter Bekannter“ von mir vorlag. Ich dachte immer an
den „schärfsten Fall“ dass  in k(
in k(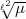 ) unzerlegt bleibt. Dann ist ja der
Restklassenkörper mod
) unzerlegt bleibt. Dann ist ja der
Restklassenkörper mod  in k(
in k(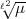 ) ein relativ cyklischer Körper vom
Grad
) ein relativ cyklischer Körper vom
Grad  2 über dem Restklassenkörper in k ; und gerade mit cyklischen
Erweiterungen vom Grad
2 über dem Restklassenkörper in k ; und gerade mit cyklischen
Erweiterungen vom Grad  2 eines Körpers der Charakteristik
2 eines Körpers der Charakteristik  (hier gibt es kein
Wurzelziehen) hatten Herr Schreier und ich uns in der Note „Eine Kennzeichnung
der reell abgeschlossenen Körper“ im vorigen Heft des Parteiblättchens,
also Bd 5 Seite 225 beschäftigt. Ich möchte bemerken, dass der in Frage
kommende Teil unabhängig ist von der Theorie der reellen Körper, also
unabhängig gelesen werden kann. Wir hatten recht lange gerechnet, bevor
wir auf alles gekommen sind und gesehen, wie schwer die Sache ist. Wir
haben dort alle cyklischen Erweiterungen dieser Art aufgestellt und die
Gleichungen bestimmt, denen die Zahlen genügen. Damit kennt man -
angewendet auf unseren Fall - natürlich noch nicht die gesuchte Zahl. Man
weiss von ihr nur, dass sie einer Kongruenz vom
(hier gibt es kein
Wurzelziehen) hatten Herr Schreier und ich uns in der Note „Eine Kennzeichnung
der reell abgeschlossenen Körper“ im vorigen Heft des Parteiblättchens,
also Bd 5 Seite 225 beschäftigt. Ich möchte bemerken, dass der in Frage
kommende Teil unabhängig ist von der Theorie der reellen Körper, also
unabhängig gelesen werden kann. Wir hatten recht lange gerechnet, bevor
wir auf alles gekommen sind und gesehen, wie schwer die Sache ist. Wir
haben dort alle cyklischen Erweiterungen dieser Art aufgestellt und die
Gleichungen bestimmt, denen die Zahlen genügen. Damit kennt man -
angewendet auf unseren Fall - natürlich noch nicht die gesuchte Zahl. Man
weiss von ihr nur, dass sie einer Kongruenz vom  2-ten Grad (diese finden
Sie in der Arbeit wenn auch nicht explizit) genügen muss denn, wenn
2-ten Grad (diese finden
Sie in der Arbeit wenn auch nicht explizit) genügen muss denn, wenn  unzerlegt bleibt, muss die Zahl eine Körpererzeugende mod
unzerlegt bleibt, muss die Zahl eine Körpererzeugende mod  sein. Ich konnte
bisher damit noch nichts anfangen. Ich bin aber überzeugt, dass es mit
sein. Ich konnte
bisher damit noch nichts anfangen. Ich bin aber überzeugt, dass es mit
 -adik gehen muss. Ich möchte noch erwähnen, dass die in der Arbeit
angegebenen Kongruenzen nachweislich die einfachsten sind. Zum Beispiel kann
man
-adik gehen muss. Ich möchte noch erwähnen, dass die in der Arbeit
angegebenen Kongruenzen nachweislich die einfachsten sind. Zum Beispiel kann
man  p-1 (wenn ich mich der Bezeichnung in der Arbeit bediene) nicht
entbehren oder durch eine niedrigere Potenz ersetzen. Ich betone das nur, um
Ihnen die Rechenarbeit zu ersparen die wir hinter uns haben und die
vergeblich war. Denn wir haben – natürlich – auch mit den kleinsten Potenzen
von
p-1 (wenn ich mich der Bezeichnung in der Arbeit bediene) nicht
entbehren oder durch eine niedrigere Potenz ersetzen. Ich betone das nur, um
Ihnen die Rechenarbeit zu ersparen die wir hinter uns haben und die
vergeblich war. Denn wir haben – natürlich – auch mit den kleinsten Potenzen
von  begonnen und haben uns überzeugt, dass es nur mit der höchsten
geht. Übrigens ist die Zahl
begonnen und haben uns überzeugt, dass es nur mit der höchsten
geht. Übrigens ist die Zahl 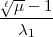 =
=  gerade das
gerade das  , denn sie genügt der
Kongruenz:
, denn sie genügt der
Kongruenz:
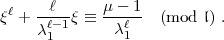 Da nun
Da nun 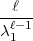
 -1
(mod
-1
(mod  )
ist, genügt
)
ist, genügt  der Kongruenz
der Kongruenz 
 -
- 

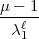 (mod
(mod  ), so dass das in unserer
Arbeit vorkommende a den Wert
), so dass das in unserer
Arbeit vorkommende a den Wert 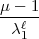 hat. Die von Ihnen gesuchte Zahl, nennen
wir sie
hat. Die von Ihnen gesuchte Zahl, nennen
wir sie 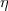 , genügt der Kongruenz:
, genügt der Kongruenz:
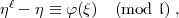 wobei
wobei 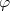 (
( ) ein Polynom (
) ein Polynom ( - 1)-ten Grades in
- 1)-ten Grades in  =
= 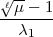 ist, nämlich eine
passende Lösung
ist, nämlich eine
passende Lösung  - 1-ten Grades der Differenzengleichung:
- 1-ten Grades der Differenzengleichung:
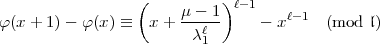 Vielleicht erleichtert es das Auffinden von
Vielleicht erleichtert es das Auffinden von 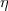 , wenn man beachtet, dass
eine passende erzeugende Substitution der Galoisgruppe die Wirkung
hat:
, wenn man beachtet, dass
eine passende erzeugende Substitution der Galoisgruppe die Wirkung
hat:
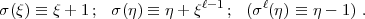 Die
Aufgabe ist nun,
Die
Aufgabe ist nun, 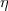 auszudrücken durch
auszudrücken durch 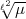 . Dazu genügt es, dass
. Dazu genügt es, dass 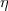 bei der
Anwendung von
bei der
Anwendung von  die angegebene Substitution erfährt.
die angegebene Substitution erfährt.
Hoffentlich können Sie etwas damit anfangen!
Mit herzlichen Grüßen
Ihr Artin
Ich danke Ihnen auch für die freundliche Übersendung der Arbeit von
Tschebotareff. Sie liegt bei. Es war ja klar, dass das schon bekannt sein
musste. Haben Sie eigentlich
die Korrekturen bekommen?
Ich frage nicht, weil ich Sie etwa mit Korrekturarbeiten belasten will, sondern weil
ich Ihnen sonst noch ein Exemplar senden müsste. Bitte fassen Sie es aber nicht
so auf, dass Sie sich bemühen. Ich bekomme demnächst die zweiten Korrekturen.
Wollen Sie ein Exemplar?
Kommentare zum Brief Nr.14:
Mit dem Ausdruck „Ge-ixe“ bezieht sich Artin auf seinen Brief Nr.12 vom
29.7.1027. Dort spricht er allerdings von einem 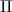 und
und 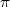 Ge-ixe; er benutzt also
hier andere Bezeichnungen.
Ge-ixe; er benutzt also
hier andere Bezeichnungen.
Mit  -Ge-ixe meint Artin offenbar das Rechnen mit
-Ge-ixe meint Artin offenbar das Rechnen mit  -adischen
Potenzreihenentwicklungen in Körpern, die die
-adischen
Potenzreihenentwicklungen in Körpern, die die  -ten Einheitswurzeln enthalten.
Dabei ist
-ten Einheitswurzeln enthalten.
Dabei ist  = 1 -
= 1 -  , unter
, unter  eine primitive
eine primitive  -te Einheitswurzel verstanden. (Das
ist die u.a. bei Hasse und Artin gängige Bezeichnungsweise.) Im Körper der
-te Einheitswurzel verstanden. (Das
ist die u.a. bei Hasse und Artin gängige Bezeichnungsweise.) Im Körper der
 n-ten Einheitswurzeln wird dann entsprechend
n-ten Einheitswurzeln wird dann entsprechend 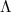 = 1 -
= 1 - 
 n gesetzt. Offenbar
ärgert sich Artin über die bei Takagi vorkommenden umständlichen Rechnungen
mit
n gesetzt. Offenbar
ärgert sich Artin über die bei Takagi vorkommenden umständlichen Rechnungen
mit  und
und 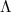 , beteuert aber, dass er grundsätzlich nicht gegen die
, beteuert aber, dass er grundsätzlich nicht gegen die  -adik von
Hensel eingestellt ist. In der Tat hatte Artin die Vorteile des Rechnens mit
-adik von
Hensel eingestellt ist. In der Tat hatte Artin die Vorteile des Rechnens mit
 -adischen Potenzreihen von Hasse gelernt; vgl. Brief Nr.4, in dem Artin
schreibt: „Ich mache langsam Fortschritte in
-adischen Potenzreihen von Hasse gelernt; vgl. Brief Nr.4, in dem Artin
schreibt: „Ich mache langsam Fortschritte in  -adik. Nun logarithmiere ich
schon!“
-adik. Nun logarithmiere ich
schon!“
 -Ge-ixe übel vermerkt. Ich wollte
damit weiss Gott nichts gegen die
-Ge-ixe übel vermerkt. Ich wollte
damit weiss Gott nichts gegen die  -adik sagen von der ich sehr wohl weiss,
dass sie für die Behandlung der Rez[iprozitäts]ges[etze] unentbehrlich
ist. Mich ärgerte nur das
-adik sagen von der ich sehr wohl weiss,
dass sie für die Behandlung der Rez[iprozitäts]ges[etze] unentbehrlich
ist. Mich ärgerte nur das  und
und 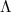 -Geixe bei Takagi an der Stelle der
Normenreste, die dort auftretenden langwierigen und doch langweiligen
Rechnungen mit Potenzsummen, das „Klettern“ auf höhere Exponenten
und all die „schönen“ Dinge. Ich glaube, da sind Sie doch auch meiner
Meinung. Dasselbe tritt dann bei den Geschlechtern nochmals auf. Was
das
-Geixe bei Takagi an der Stelle der
Normenreste, die dort auftretenden langwierigen und doch langweiligen
Rechnungen mit Potenzsummen, das „Klettern“ auf höhere Exponenten
und all die „schönen“ Dinge. Ich glaube, da sind Sie doch auch meiner
Meinung. Dasselbe tritt dann bei den Geschlechtern nochmals auf. Was
das  -Ge-ixe bei der Ranguntersuchung betrifft, so beachten Sie bitte:
Es ist nur ein „klein-
-Ge-ixe bei der Ranguntersuchung betrifft, so beachten Sie bitte:
Es ist nur ein „klein- “-Ge-ixe und nicht allzulang; bei weitem nicht so
hässlich wie bei den Normenresten. Was dann die relativen Grundeinheiten
betrifft101 ,
so kommt mein ganz besonderer Zorn auf sie daher, weil ich mich im
Kolleg zweimal verheddert habe und erst nach dem dritten Mal alles
einwandfrei erledigte. Mein besonderer Fluch gilt dem Symbol [
“-Ge-ixe und nicht allzulang; bei weitem nicht so
hässlich wie bei den Normenresten. Was dann die relativen Grundeinheiten
betrifft101 ,
so kommt mein ganz besonderer Zorn auf sie daher, weil ich mich im
Kolleg zweimal verheddert habe und erst nach dem dritten Mal alles
einwandfrei erledigte. Mein besonderer Fluch gilt dem Symbol [ ], dessen
besondere Tücken sich – natürlich – im Fall
], dessen
besondere Tücken sich – natürlich – im Fall  = 2 offenbaren. Wissen Sie
wenigstens in diesem Fall ein einfaches Hilfsmittel? Man muss da schrecklich
„klettern“.
= 2 offenbaren. Wissen Sie
wenigstens in diesem Fall ein einfaches Hilfsmittel? Man muss da schrecklich
„klettern“.
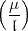 im Fall
im Fall 
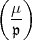 meistens so)
meistens so) 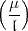 ist doch
neu? Vielleicht ist es Ihnen aber doch nützlich, wenn auch vielleicht nicht
neu, wenn ich Ihnen meine „Erfahrungen“ über
ist doch
neu? Vielleicht ist es Ihnen aber doch nützlich, wenn auch vielleicht nicht
neu, wenn ich Ihnen meine „Erfahrungen“ über 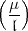 schreibe. Ich habe
nur den Fall
schreibe. Ich habe
nur den Fall 



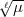
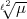
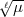
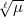
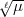
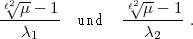
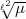
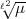
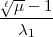
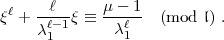
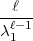
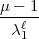
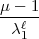 hat. Die von Ihnen gesuchte Zahl, nennen
wir sie
hat. Die von Ihnen gesuchte Zahl, nennen
wir sie 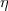
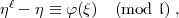
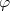
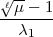 ist, nämlich eine
passende Lösung
ist, nämlich eine
passende Lösung