 n. Der Grundkörper k enthalte die m-ten Einheitswurzeln. Das Primideal
n. Der Grundkörper k enthalte die m-ten Einheitswurzeln. Das Primideal  sei im Körper K = k(
sei im Körper K = k(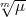 ) unverzweigt, d.h.
) unverzweigt, d.h.  sei „primär“ für
sei „primär“ für  . Dann ist nach
Hasse das erweiterte Potenzrestsymbol
. Dann ist nach
Hasse das erweiterte Potenzrestsymbol 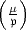 durch die folgende Formel definiert
(siehe 10.2):
durch die folgende Formel definiert
(siehe 10.2):
Es geht um das Potenzrestsymbol für einen Primzahlpotenz-Exponenten
m =  n. Der Grundkörper k enthalte die m-ten Einheitswurzeln. Das Primideal
n. Der Grundkörper k enthalte die m-ten Einheitswurzeln. Das Primideal  sei im Körper K = k(
sei im Körper K = k(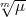 ) unverzweigt, d.h.
) unverzweigt, d.h.  sei „primär“ für
sei „primär“ für  . Dann ist nach
Hasse das erweiterte Potenzrestsymbol
. Dann ist nach
Hasse das erweiterte Potenzrestsymbol 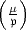 durch die folgende Formel definiert
(siehe 10.2):
durch die folgende Formel definiert
(siehe 10.2):
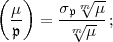 | (26) |
wobei 
 den zu
den zu  gehörigen Frobenius-Automorphismus bedeutet. Wenn
gehörigen Frobenius-Automorphismus bedeutet. Wenn  nicht
in m aufgeht, dann kann
nicht
in m aufgeht, dann kann 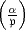 auch durch die klassische Eulersche Kongruenz
charakterisiert werden (siehe (1), Seite 54):
auch durch die klassische Eulersche Kongruenz
charakterisiert werden (siehe (1), Seite 54):
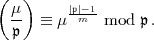 | (27) |
Dies ist die Formel, die meist in den gängigen Darstellungen der klassischen
Reziprozitätgesetze angegeben wird. Sie versagt jedoch wenn  ein Primidealteiler
von
ein Primidealteiler
von  ist. Die Primteiler von
ist. Die Primteiler von  im Körper k werden bei Artin und Hasse stets mit
im Körper k werden bei Artin und Hasse stets mit
 bezeichnet. Im Zusammenhang mit dem zweiten Ergänzungssatz zum
Reziprozitätsgesetz sucht man nun nach einer Kongruenz modulo einer geeigneten
Potenz von
bezeichnet. Im Zusammenhang mit dem zweiten Ergänzungssatz zum
Reziprozitätsgesetz sucht man nun nach einer Kongruenz modulo einer geeigneten
Potenz von  , die das Potenzrestsymbol
, die das Potenzrestsymbol 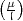 in entsprechender Weise
kennzeichnet – immer unter der Voraussetzung, dass
in entsprechender Weise
kennzeichnet – immer unter der Voraussetzung, dass  in k(
in k(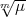 ) unverzweigt, also
) unverzweigt, also
 primär für
primär für  ist.
ist.
Für den Fall n = 1 (also m =  ) hat Hasse in
[Has27e]111
eine solche Formel gefunden, nämlich
) hat Hasse in
[Has27e]111
eine solche Formel gefunden, nämlich
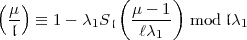 | (28) |
mit folgenden Bezeichnungen:112
Es wird dabei vorausgesetzt, dass 
 1 mod
1 mod 
 1, was keine wesentliche Einschränkung
bedeutet. Denn
1, was keine wesentliche Einschränkung
bedeutet. Denn  ist genau dann primär für m =
ist genau dann primär für m =  , wenn
, wenn  bis auf einen
bis auf einen
 -Potenzfaktor der Kongruenz
-Potenzfaktor der Kongruenz 
 1 mod
1 mod 
 1 genügt.
1 genügt.
Artin sagt in seinem Brief, dass er auch schon über eine solche Formel
nachgedacht habe, dass er sich aber noch nicht überlegt habe, „welche
Zahl zu nehmen ist“. Diese „Zahl“ ist nun nach Hasse  =
= 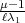 . Artin
bezeichnet die Formel (28) als „schöne“ Formel und fragt, ob sie neu
ist.113
In Artins Brief wird die Formel nicht explizit hingeschrieben, er bezieht sich auf
Hasses vorangegangenen Brief, den wir nicht kennen. Hasse hatte diese Formel
offenbar in seinem Brief mitgeteilt; möglicherweise hatte Hasse sogar schon das
Manuskript seiner Arbeit [Has27e] fertiggestellt und Artin eine Kopie oder die
Korrekturfahnen dazu geschickt.
. Artin
bezeichnet die Formel (28) als „schöne“ Formel und fragt, ob sie neu
ist.113
In Artins Brief wird die Formel nicht explizit hingeschrieben, er bezieht sich auf
Hasses vorangegangenen Brief, den wir nicht kennen. Hasse hatte diese Formel
offenbar in seinem Brief mitgeteilt; möglicherweise hatte Hasse sogar schon das
Manuskript seiner Arbeit [Has27e] fertiggestellt und Artin eine Kopie oder die
Korrekturfahnen dazu geschickt.
Wie Hasse in der genannten Crelle-Arbeit zeigt, kann man der Formel (28) auch die Form
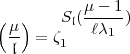 | (29) |
geben. Vielleicht war es diese, die Artin als „schöne Formel“ bezeichnete?
Die Formeln (28), (29) gelten, wie gesagt, für einen Primzahlexponenten
m =  . Artin diskutiert in seinem Brief nun einen Ansatz für m =
. Artin diskutiert in seinem Brief nun einen Ansatz für m =  2.
Wir können annehmen, dass Hasse angefragt hatte, ob Artin eine Idee
hätte, wie man die Formeln für Primzahlpotenz-Exponenten m =
2.
Wir können annehmen, dass Hasse angefragt hatte, ob Artin eine Idee
hätte, wie man die Formeln für Primzahlpotenz-Exponenten m =  n mit
beliebigem n verallgemeinern könnte, und dass dies die Antwort von Artin
ist.
n mit
beliebigem n verallgemeinern könnte, und dass dies die Antwort von Artin
ist.
In seiner Diskussion setzt Artin voraus, nicht nur dass  unverzweigt ist
in k(
unverzweigt ist
in k(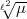 ), sondern auch, dass
), sondern auch, dass  in k(
in k(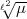 ) unzerlegt ist; das bedeutet,
dass der Trägheitsgrad den maximalen Wert
) unzerlegt ist; das bedeutet,
dass der Trägheitsgrad den maximalen Wert  2 annimmt und also die
Frobenius-Substitution
2 annimmt und also die
Frobenius-Substitution 
 die Ordnung
die Ordnung  2 besitzt. Artin bezeichnet dies als den
„schärfsten Fall.“
2 besitzt. Artin bezeichnet dies als den
„schärfsten Fall.“
Es ist nun außerordentlich bemerkenswert und von großer Tragweite, dass
Artin ein Resultat ins Spiel bringt, das er vor kurzem zusammen mit Otto
Schreier in einem völlig anderen Zusammenhang erarbeitet hatte, nämlich die
heute so genannte Artin-Schreier-Erzeugung von zyklischen Körpern  -ten Grades
der Charakteristik
-ten Grades
der Charakteristik  . Dieses Resultat ist enthalten in der Arbeit „Eine
Kennzeichnung der reell abgeschlossenen Körper“ [AS27], die soeben im, wie
Artin sagt, „Parteiblättchen“ erschienen war, also in den Hamburger
Abhandlungen. Artin bemerkt, dass die Zahl
. Dieses Resultat ist enthalten in der Arbeit „Eine
Kennzeichnung der reell abgeschlossenen Körper“ [AS27], die soeben im, wie
Artin sagt, „Parteiblättchen“ erschienen war, also in den Hamburger
Abhandlungen. Artin bemerkt, dass die Zahl
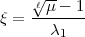
aus dem Körper k(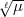 ) in dessen Restklassenkörper gerade eine
Artin-Schreier-Erzeugende liefert und gibt die zugehörige Kongruenz mod
) in dessen Restklassenkörper gerade eine
Artin-Schreier-Erzeugende liefert und gibt die zugehörige Kongruenz mod  explizit an, nämlich
explizit an, nämlich
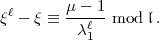
Diese Kongruenz findet sich übrigens auch in der o.g. Arbeit von Hasse [Has27e], ohne allerdings dass Hasse den Zusammenhang mit der Artin-Schreier-Theorie erwähnte, die er damals wahrscheinlich noch nicht gekannt hatte.
Der Artinsche Ansatz im vorliegenden Brief geht nun davon aus, dass er in der
erwähnten Arbeit mit Schreier auch zyklische Körpererweiterungen von Grad  2
in Charakteristik
2
in Charakteristik  behandelt hatte. In der Tat hatten Artin und Schreier gezeigt,
dass in Charakteristik
behandelt hatte. In der Tat hatten Artin und Schreier gezeigt,
dass in Charakteristik  jede zyklische Erweiterung vom Grad
jede zyklische Erweiterung vom Grad  in eine zyklische
Erweiterung vom Grad
in eine zyklische
Erweiterung vom Grad  2 eingebettet werden kann, und sie hatten die Bedingung
für die zugehörigen Artin-Schreier-Erzeugenden
2 eingebettet werden kann, und sie hatten die Bedingung
für die zugehörigen Artin-Schreier-Erzeugenden 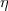 in der zweiten Stufe angegeben.
Die Arbeit von Artin-Schreier war zum Zeitpunkt der Abfassung des
vorliegenden Briefes noch so frisch, dass Artin bei Hasse nicht deren Kenntnis
voraussetzen konnte; deshalb erläutert er in seinem Brief den Sachverhalt
genauer.
in der zweiten Stufe angegeben.
Die Arbeit von Artin-Schreier war zum Zeitpunkt der Abfassung des
vorliegenden Briefes noch so frisch, dass Artin bei Hasse nicht deren Kenntnis
voraussetzen konnte; deshalb erläutert er in seinem Brief den Sachverhalt
genauer.
Artin spricht von „der von Ihnen gesuchten Zahl“. Offenbar suchte Hasse eine
Zahl 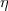 , die im Falle m =
, die im Falle m =  2 denselben Dienst leistet wie das obige
2 denselben Dienst leistet wie das obige  im
Falle m =
im
Falle m =  . Artin gibt nun einen Ansatz für die Zahl
. Artin gibt nun einen Ansatz für die Zahl 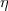 , indem er die
Kongruenzeigenschaften von
, indem er die
Kongruenzeigenschaften von 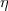 modulo
modulo  beschreibt, gestützt auf die Ergebnisse
der Artin-Schreier-Arbeit. Aber er gibt keine explizite Form für ein solches
beschreibt, gestützt auf die Ergebnisse
der Artin-Schreier-Arbeit. Aber er gibt keine explizite Form für ein solches 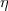 an, er hofft nur, dass Hasse mit diesen Eigenschaften „etwas anfangen
kann“.
an, er hofft nur, dass Hasse mit diesen Eigenschaften „etwas anfangen
kann“.
Als Nebenbemerkung erfahren wir, dass Artin und Schreier viel gerechnet hatten, um zu ihrem in der Publikation so einfach erscheinenden und einleuchtenden Ergebnis für zyklische Körper in Primzahl-Charakteristik zu kommen. Artin spricht von der „Rechenarbeit, die wir hinter uns haben, und die vergeblich war“.
Wie es scheint, wurde der Ansatz von Artin zunächst nicht weiter verfolgt,
weder von Hasse noch von Artin selbst. Ein Grund wird wohl gewesen
sein, dass man die Erzeugung der zyklischen Körper vom  -Potenzgrad
-Potenzgrad
 n in Charakteristik
n in Charakteristik  für n > 2 noch nicht im Detail beherrschte.
Einige Jahre später gab Albert (der mit Hasse in Briefwechsel stand)
einen Mechanismus an, wie solche Körper zu erzeugen sind. Er schrieb am
6.2.1934:114
für n > 2 noch nicht im Detail beherrschte.
Einige Jahre später gab Albert (der mit Hasse in Briefwechsel stand)
einen Mechanismus an, wie solche Körper zu erzeugen sind. Er schrieb am
6.2.1934:114
„Dear Professor Hasse, I am happy to be able to write to you of my success in generalizing the Artin-Schreier results…“.
Albert publizierte seine Resultate 1934 im Bulletin of the AMS [Alb34]. Wiederum einige Zeit später entwickelte H.L.Schmid im Rahmen seiner (von Hasse angeregten) Untersuchungen zum Reziprozitätsgesetz in algebraischen Funktionenkörpern eine Variante der Albertschen Konstruktion, die zwar substantiell dasselbe lieferte jedoch formale Vereinfachungen beinhaltete [Sch36]. Diese Konstruktion von H.L.Schmid wurde dann von Witt als die heute sogenannte „Wittsche Vektorrechnung“ erkannt [Wit37]. Die Resultate von H.L.Schmid und Witt wurden 1936 in der Göttinger Arbeitsgemeinschaft für Algebra und Zahlentheorie vorgetragen; sie erschienen 1937 im Crelleschen Journal.
Als Hasse in jener Arbeitsgemeinschaft die Wittsche Vektorrechnung
kennenlernte, da griff er sie sofort auf, um damit das Problem, das sich aus dem
hier vorliegenden Artinschen Brief ergab und bis dahin ungelöst war, in Angriff zu
nehmen. Im selben Heft des Crelleschen Journals, in dem auch die Arbeit über
Wittsche Vektoren erschien, publizierte Hasse seine Lösung, indem er die
Formel (29) für einen beliebigen Primzahlpotenz-Exponenten  n statt nur
n statt nur  verallgemeinerte [Has37]. Die Verallgemeinerung sieht äußerlich ganz ähnlich aus
wie (29), jedoch ist statt der Zahl
verallgemeinerte [Has37]. Die Verallgemeinerung sieht äußerlich ganz ähnlich aus
wie (29), jedoch ist statt der Zahl  =
= 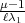 ein Witt-Vektor
ein Witt-Vektor  zu nehmen,
dessen erste n Komponenten den Restklassenkörper erzeugen, und der
nach Witt als ganze
zu nehmen,
dessen erste n Komponenten den Restklassenkörper erzeugen, und der
nach Witt als ganze  -adische Zahl über dem Restklassenkörper von k
zu interpretieren ist. Dazu muss Hasse zunächst die Potenzierung von
-adische Zahl über dem Restklassenkörper von k
zu interpretieren ist. Dazu muss Hasse zunächst die Potenzierung von
 -adischen Einseinheiten mit solchen Wittschen Vektoren in geeigneter
Weise definieren. In diesem Sinne hat sich also die Ahnung von Artin
bewahrheitet, wenn er schreibt: „Ich bin aber überzeugt, dass es mit
-adischen Einseinheiten mit solchen Wittschen Vektoren in geeigneter
Weise definieren. In diesem Sinne hat sich also die Ahnung von Artin
bewahrheitet, wenn er schreibt: „Ich bin aber überzeugt, dass es mit  -adik gehen
muss.“
-adik gehen
muss.“
In derselben Arbeit [Has37] gelingt es Hasse auch, das von Artin angeschnittene
Problem der Beschreibung „primärer“ Zahlen  für
für  zu lösen. Artin schreibt ja
richtig, dass die von Hasse angegebene Kongruenz
zu lösen. Artin schreibt ja
richtig, dass die von Hasse angegebene Kongruenz 
 x
x 2
(mod
2
(mod  2
2 1) zwar
hinreichend aber nicht notwendig sei dafür, dass es sich bei
1) zwar
hinreichend aber nicht notwendig sei dafür, dass es sich bei  um eine
um eine  2-primäre
Zahl (für
2-primäre
Zahl (für  ) handelt, d.h. dass
) handelt, d.h. dass  in k(
in k(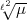 ) unverzweigt ist. Das Problem der
Bestimmung
) unverzweigt ist. Das Problem der
Bestimmung  n-primärer Zahlen für n > 2 wird von Artin wiederum in einem der
folgenden Briefe angeschnitten (nämlich in Nr.16 vom 4.9.1927) jedoch erst mit
der Hasseschen Arbeit [Has37] gelöst. Demgemäß trägt jene Arbeit auch den
Titel: „Die Gruppe der pn-primären Zahlen für einen Primteiler
n-primärer Zahlen für n > 2 wird von Artin wiederum in einem der
folgenden Briefe angeschnitten (nämlich in Nr.16 vom 4.9.1927) jedoch erst mit
der Hasseschen Arbeit [Has37] gelöst. Demgemäß trägt jene Arbeit auch den
Titel: „Die Gruppe der pn-primären Zahlen für einen Primteiler  von
p.“
von
p.“
Im Falle n = 1 war das Resultat wohlbekannt, denn Wittsche Vektoren der Länge 1 sind nichts anderes als Zahlen des Körpers. Hasse verweist in Teil Ia seines Klassenkörperberichts auf Heckes Buch über algebraische Zahlen [Hec23].
Wir sehen, dass diese hochinteressanten Entwicklungen ihren Ursprung in dem vorliegenden Brief von Artin hatten, der auf den Zusammenhang mit den sogenannten Artin-Schreier-Erzeugenden in Primzahlcharakteristik hinwies. Später, im Jahre 1949, nahm I.R.Shafarevich115 [Sha51] die Fragestellung wieder auf und führte die Hasseschen Untersuchungen zu einem gewissen Abschluss. Die Arbeit erschien 1951 auf Russisch in den Doklady Akad. Nauk. SSSR; eine ausführliche Darstellung auf Deutsch gab Hasse im selben Jahr [Has51a]. Ebenfalls im selben Jahr 1951 gab Martin Kneser [Kne51] eine vereinfachte Darstellung; vgl. dazu auch das zugehörige Zentralblatt-Referat von Witt. Die Arbeit von Shafarevich wurde 1956 von Emma Lehmer ins Englische übersetzt [Sha56].