 n-primär
und
n-primär
und 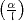 haben mich so geärgert, dass ich beschloss spezielle Fälle
auszurechnen.137
haben mich so geärgert, dass ich beschloss spezielle Fälle
auszurechnen.137
Hamburg, am 4. September
1927 135
Lieber Herr Hasse!
Ich bin in grosser Sorge dass Sie meinetwegen Ihre ganzen Pläne umwerfen müssen und ich möchte Sie bitten das doch nicht zu tun, sondern mir einfach abzuschreiben wenn es Ihnen nicht passt. Mein jetziger endgültiger Reiseplan hat sich nun etwas verschoben. Ich fahre am Dienstag den 13.September, vermutlich morgens hier ab und bin so gegen halb eins in Halle. Die genaue Zeit schreibe ich noch. Es würde nun von Ihrer Zeit abhängen, ob ich Sie einen oder zwei Tage in Anspruch nehmen darf. Aber bitte doch ja nichts meinetwegen zu verschieben. Ihre Angelegenheiten gehen doch selbstverständlich vor und passt es Ihnen jetzt nicht, so lässt sich doch vielleicht auf meiner Rückreise etwas machen. Darf ich Sie bitten, mir noch zu schreiben ob es Ihnen zur angegebenen Zeit passt und entschuldigen Sie mein andauerndes Verschieben des Datums. Jetzt steht es fest. Haben Sie auch nochmals herzlichen Dank für die freundliche Einladung. 136
In den letzten Tagen bin ich zu nichts gekommen aber vor acht Tagen
bin ich unter die Rechner gegangen. Die ganzen Dinge mit  n-primär
und
n-primär
und 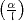 haben mich so geärgert, dass ich beschloss spezielle Fälle
auszurechnen.137
haben mich so geärgert, dass ich beschloss spezielle Fälle
auszurechnen.137
Ich nahm die Fälle 4, 8, 9 im Körper der zugehörigen Einheitswurzeln. Die Resultate sind diese:
Ist  n = e2
n = e2 i/
i/ n
, so dass also
n
, so dass also  n-1 =
n-1 =  n
n etc. ist und wird
etc. ist und wird  n = 1 -
n = 1 - n gesetzt,
so gilt der zweite Ergänzungssatz in der bekannten, leicht verallgemeinerten
Fassung.
n gesetzt,
so gilt der zweite Ergänzungssatz in der bekannten, leicht verallgemeinerten
Fassung.
Für 
 1 (mod
1 (mod  n) im Körper R(
n) im Körper R( n) gilt:
n) gilt:
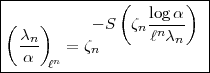
Für den Fall  2 kann ich aber wenigstens allgemein zeigen, dass:
2 kann ich aber wenigstens allgemein zeigen, dass:
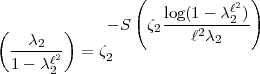
 na) für a <
na) für a <  n mit zu
n mit zu  primen a und noch (1 -
primen a und noch (1 - n
n n
)
eine multiplikative Basis bilden (Ersatz für Takagische Basis), so ist gezeigt, dass
im Fall
n
)
eine multiplikative Basis bilden (Ersatz für Takagische Basis), so ist gezeigt, dass
im Fall  2 die obige Formel für das letzte Basiselement (1 -
2 die obige Formel für das letzte Basiselement (1 -  2
2 2
) gilt. Da
nun
2
) gilt. Da
nun
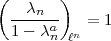
 , so hat man noch zu beweisen:
, so hat man noch zu beweisen:
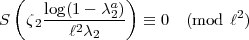
 ) = 1. Wenn das gezeigt ist, hat man die Formel allgemein. Das aber kann ich
nicht (oder nur für 4,8,9).
) = 1. Wenn das gezeigt ist, hat man die Formel allgemein. Das aber kann ich
nicht (oder nur für 4,8,9).
Für  3 kann ich aber nicht einmal mehr zeigen dass die Formel für (1 -
3 kann ich aber nicht einmal mehr zeigen dass die Formel für (1 -  3
3 3
)
stimmt.
3
)
stimmt.
Ich bin jetzt fest überzeugt, dass dies der zweite Ergänzungssatz im
Kreiskörper ist und bin über die einfache Bauart dieser Formel ausserordentlich
erstaunt. Wenn nun  primär ist, so folgt aus Ihrer Formulierung des
R[eziprozitäts]g[esetzes]138 ,
dass
primär ist, so folgt aus Ihrer Formulierung des
R[eziprozitäts]g[esetzes]138 ,
dass 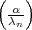 durch dieselbe Formel gegeben ist.
durch dieselbe Formel gegeben ist.
Weitere Fälle wie 27, 25, 49, 16 ect. auszurechnen ohne allgemeine
Methode, übersteigt meine rechnerische Geduld, da das dazu erforderliche
Berechnen von S( ni) für zu grosse Werte von i notwendig wird und
bereits für 8 und 9 sehr langweilig ist. Hoffentlich fällt Ihnen da etwas
ein.139
ni) für zu grosse Werte von i notwendig wird und
bereits für 8 und 9 sehr langweilig ist. Hoffentlich fällt Ihnen da etwas
ein.139
Für das R[eziprozitäts]g[esetz] selbst gilt sicher eine ähnliche Formel wie die von Ihnen aufgestellte, doch habe ich sie mir nicht überlegt. Sie ist ganz bestimmt nicht irgendwie komplizierter und das ist doch erstaunlich.
Aber was  n-primär ist, weiss ich für 4, 8, 9. Ich habe mich bemüht eine
gemeinsame Formel für die drei Fälle zu finden und fand nur die folgende, von der
ich aber überzeugt bin, dass sie nicht die allgemeine ist, da ich schon ihre
Invarianz gegen Substitutionen des Körpers bezweifle. Immerhin gebe ich sie in
der fraglichen Form schon der Abkürzung halber.
n-primär ist, weiss ich für 4, 8, 9. Ich habe mich bemüht eine
gemeinsame Formel für die drei Fälle zu finden und fand nur die folgende, von der
ich aber überzeugt bin, dass sie nicht die allgemeine ist, da ich schon ihre
Invarianz gegen Substitutionen des Körpers bezweifle. Immerhin gebe ich sie in
der fraglichen Form schon der Abkürzung halber.
Für  n = 4, 8 und 9 ist
n = 4, 8 und 9 ist  eine
eine  n-primäre Zahl, wenn (für
n-primäre Zahl, wenn (für 
 1
(mod
1
(mod  n))
n))
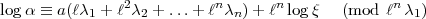

 1 (mod
1 (mod n) irgend eine Zahl des
Kreiskörpers.
n) irgend eine Zahl des
Kreiskörpers.
Ich bin aber überzeugt, dass das nicht allgemein stimmt, da sie nur für 4,8,9
invariant ist. Vielleicht fällt Ihnen aber jetzt die richtige Verallgemeinerung ein.
Das Glied  n log
n log  rührt natürlich von dem Beitrag
rührt natürlich von dem Beitrag 
 n
bei
n
bei  her und ist für n > 1
keineswegs zu vernachlässigen. Vielleicht kann man mit seiner Hilfe der ersten
Klammer die „richtige“ Gestalt geben.
her und ist für n > 1
keineswegs zu vernachlässigen. Vielleicht kann man mit seiner Hilfe der ersten
Klammer die „richtige“ Gestalt geben.
Ich habe bei meinen mannigfachen Versuchen gesehen, wie schwer die Dinge mit
der bisherigen  -adik sind. Ein Jammer, dass man nichts vernünftiges mit
-adik sind. Ein Jammer, dass man nichts vernünftiges mit 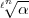 anfangen kann, da ja die Reihe nicht immer konvergiert. Ebenso, dass es keine
Formel gibt um stets vom log
anfangen kann, da ja die Reihe nicht immer konvergiert. Ebenso, dass es keine
Formel gibt um stets vom log  zu
zu  zu gelangen, da wieder elog
zu gelangen, da wieder elog  nicht immer
konvergiert.140
nicht immer
konvergiert.140
Mit der Henselschen Arbeit über diese Frage kann ich auch nichts anfangen. Aber da wissen Sie ja besser Bescheid. 141
Mit vielen Grüssen und einer Empfehlung an Frau Gemahlin
Ihr Artin
Es scheint mir als wäre allgemein für primäres
 : 142
: 142
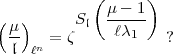
Kommentare zum Brief Nr.16: