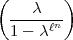 , da sie mir gleich eine Vermutung =
, da sie mir gleich eine Vermutung =  ±1 widerlegt. Die
Arbeit kommt in unser nächstes Heft, mit dessen Druck bald begonnen
wird. 146
±1 widerlegt. Die
Arbeit kommt in unser nächstes Heft, mit dessen Druck bald begonnen
wird. 146
Lieber Herr Hasse!
Ich bin leider erst vorgestern wieder hier
angekommen145 ,
so dass ich erst jetzt Ihre Sendung hier vorfand. Besten Dank. Ich wüsste nicht
was ich am Manuskript ändern sollte. Einige kleine Bemerkungen die ich
Ihnen noch schreiben wollte fand ich von selbst darin vor, so dass sich
auch das erübrigt hat. Neu und amüsant finde ich auch noch Ihre letzte
Rechnung 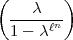 , da sie mir gleich eine Vermutung =
, da sie mir gleich eine Vermutung =  ±1 widerlegt. Die
Arbeit kommt in unser nächstes Heft, mit dessen Druck bald begonnen
wird. 146
±1 widerlegt. Die
Arbeit kommt in unser nächstes Heft, mit dessen Druck bald begonnen
wird. 146
Nun muss ich noch Ihren letzten Brief nach Reichenberg
beantworten.147
Mich haben die Ausführungen sehr interessiert, vor allem deshalb, weil sie
doch zeigen dass man möglicherweise durchkommt. Man müsste meines
Erachtens einmal die ganze Primzahltheorie mit 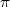 (x) < ? durchackern
statt mit
(x) < ? durchackern
statt mit 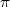 (x) = A + O( ) und die Abschätzungen so gut wie möglich
machen. Einerseits ist es wegen des fehlenden sehr bequemen O schwerer,
andrerseits aber leichter als ich ursprünglich dachte, da ich glaubte, man
müsse die Konstante im O-Glied bestimmen. Es genügt aber schon ein
(x) = A + O( ) und die Abschätzungen so gut wie möglich
machen. Einerseits ist es wegen des fehlenden sehr bequemen O schwerer,
andrerseits aber leichter als ich ursprünglich dachte, da ich glaubte, man
müsse die Konstante im O-Glied bestimmen. Es genügt aber schon ein
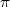 (x) < und das ist viel einfacher. Leider habe ich momentan keinen
Doktoranden, der sich für diese Dinge interessiert. Wie steht es damit bei
Ihnen?
(x) < und das ist viel einfacher. Leider habe ich momentan keinen
Doktoranden, der sich für diese Dinge interessiert. Wie steht es damit bei
Ihnen?
Auch ich habe mich übrigens (ohne Erfolg) um 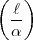 und
und 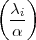 bemüht. Es
wird wohl keine einfache Formel geben.
bemüht. Es
wird wohl keine einfache Formel geben.
Ich komme jetzt zu Ihrem letzten Brief. Ich muss sagen, da staune ich. Erstens dass Sie auf dem Wege durchgekommen sind (ich hätte das garnicht gewagt) und zweitens über die merkwürdige Bauart der Formel.148 Ich konnte bisher natürlich noch nicht über sie nachdenken, Sie wissen ja, wie es in den ersten Tagen nach der Rückkehr zugeht, aber hoffe in den nächsten Tagen dazu zu kommen. Bis dahin sind Sie ja natürlich schon wieder viel weiter gekommen. Denn wenn Sie einmal so weit sind, wird es auch noch gehen. Ich bin schon ausserordentlich gespannt auf Ihren nächsten Brief.
Hecke habe ich vom zweiten Erg[änzungs]satz erzählt. Er war sehr erstaunt darüber dass es geht. Ich muss ja nun doch sagen, dass wir ein bisschen Glück bei der Sache hatten.
Ich lege Ihnen den versprochenen Beweis über die Einheiten in Körpern bei. Sie erinnern sich wohl noch. Hoffentlich gefällt Ihnen die Anordnung. 149
Nun muss ich Ihnen nochmals meinen herzlichen Dank aussprechen für die liebenswürdige und grosse Gastfreundschaft. Ich habe noch die ganze Zeit im langweiligen Reichenberg davon geschwelgt.
Hoffentlich kann ich nun bald wieder an die Arbeit kommen und Ihnen was ordentliches erzählen.
Mit einer Empfehlung an Frau Gemahlin und besten Grüssen
Ihr Artin
Darf man Ihnen schon gratulieren? 150
Beilage zum Brief Nr.17:
Ich schicke einen von Minkowski stammenden Hilfssatz voraus:
Hilfssatz: Die Matrix (aik)i,k=1,…,r habe folgende Eigenschaften: aii > 0
dagegen aik < 0 für i≠k, und ferner für jedes k sei 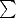
 =1ra
=1ra k > 0. Dann gilt:
|aik|≠0.
k > 0. Dann gilt:
|aik|≠0.
Beweis: (von Furtwängler) Andernfalls wäre das Gleichungssystem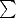 k=1raiktk = 0 (i = 1,…,r) in nicht trivialer Weise lösbar. Man darf
annehmen, dass unter den ti positive Zahlen vorkommen und zwar (wegen der
Symmetrie der Voraussetzungen), dass etwa t1,t2,…,ts > 0 sind, dagegen alle
übrigen < 0.
k=1raiktk = 0 (i = 1,…,r) in nicht trivialer Weise lösbar. Man darf
annehmen, dass unter den ti positive Zahlen vorkommen und zwar (wegen der
Symmetrie der Voraussetzungen), dass etwa t1,t2,…,ts > 0 sind, dagegen alle
übrigen < 0.
Man addiere die ersten s Gleichungen und erhält:
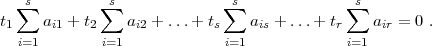 | (1) |
Was weiss man nun über 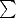 i=1saik ? Wäre die Summe bis r erstreckt, so wäre
sie nach Annahme > 0. Wenn nun k < s sind, fehlen in der tatsächlich
vorkommenden Summe nur negative Glieder, sie ist also erst recht > 0. Für k > s
aber besteht die Summe aus lauter negativen Gliedern, sie ist also < 0. Nun
erkennt man, dass in (1) kein Glied linker Hand negativ, die ersten s Glieder
sogar positiv sind. Widerspruch! q.e.d.
i=1saik ? Wäre die Summe bis r erstreckt, so wäre
sie nach Annahme > 0. Wenn nun k < s sind, fehlen in der tatsächlich
vorkommenden Summe nur negative Glieder, sie ist also erst recht > 0. Für k > s
aber besteht die Summe aus lauter negativen Gliedern, sie ist also < 0. Nun
erkennt man, dass in (1) kein Glied linker Hand negativ, die ersten s Glieder
sogar positiv sind. Widerspruch! q.e.d.
Es sei jetzt k unser Zahlkörper n-ten Grades und  1,
1, 2,…,
2,…, n eine
Minimalbasis. Man fasse die
n eine
Minimalbasis. Man fasse die  i als hyperkomplexe Zahlen auf und bilde bei
beliebigen reellen xi die Zahl
i als hyperkomplexe Zahlen auf und bilde bei
beliebigen reellen xi die Zahl
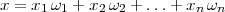
Wir erweitern vorübergehend den Begriff „Hauptideal“ indem wir auch das
von x erzeugte Hauptideal ins Auge fassen. Es bestehe (x) aus allen Vielfachen
von x, also x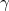 , wo
, wo 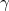 alle ganzen Körperzahlen durchläuft. Wenn x selbst ganze
oder gebrochene Körperzahl ist, bildet (x) ein Gitter mit dem Maschenvolumen
|Nx|. Ist x beliebig, so gilt aus Stetigkeitsgründen dasselbe (in der Nähe von x
liegen Körperzahlen) nur muss, damit ein Gitter entsteht, natürlich Nx≠0
sein.
alle ganzen Körperzahlen durchläuft. Wenn x selbst ganze
oder gebrochene Körperzahl ist, bildet (x) ein Gitter mit dem Maschenvolumen
|Nx|. Ist x beliebig, so gilt aus Stetigkeitsgründen dasselbe (in der Nähe von x
liegen Körperzahlen) nur muss, damit ein Gitter entsteht, natürlich Nx≠0
sein.
Man betrachte nun ( =
=  1
1 1 + … +
1 + … +  n
n n gesetzt, wo
n gesetzt, wo  wieder eine beliebige
allgemeine Zahl ist) den Würfel |
wieder eine beliebige
allgemeine Zahl ist) den Würfel | i|<
i|<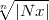 . Sein Volumen ist 2n |Nx| so dass
er einen vom Ursprung verschiedenen Gitterpunkt des Ideals (x) enthält.
Also gibt es ein ganzes
. Sein Volumen ist 2n |Nx| so dass
er einen vom Ursprung verschiedenen Gitterpunkt des Ideals (x) enthält.
Also gibt es ein ganzes 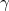 ≠0 aus k, so dass,
≠0 aus k, so dass,  = x
= x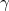 gesetzt, |
gesetzt, | i|<
i|<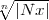 ist.
ist.
Nun ist N eine ganze rationale homogene Funktion n-ten Grades in den
eine ganze rationale homogene Funktion n-ten Grades in den  i.
Ist also C das Maximum von |N
i.
Ist also C das Maximum von |N | für |
| für | i|< 1, so ist C . hn das Maximum von
|N
i|< 1, so ist C . hn das Maximum von
|N | für |
| für | i|< h. Also gilt:
i|< h. Also gilt:
Es gibt eine nur von k abhängige Zahl C, von der Art, dass bei beliebigem x
eine ganze Zahl 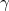 existiert so dass für
existiert so dass für  = x
= x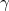 gilt:
gilt:
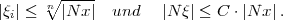 | (2) |
Daraus folgt |Nx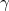 |< C .|Nx|, also |N
|< C .|Nx|, also |N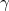 |< C .
|< C .
Man betrachte nun (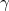 hängt ja noch von x ab) die von den möglichen
hängt ja noch von x ab) die von den möglichen 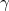 erzeugten Hauptideale (
erzeugten Hauptideale (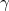 ). Da sie von beschränkter Norm sind, gibt es nur
endlich viele, etwa: (
). Da sie von beschränkter Norm sind, gibt es nur
endlich viele, etwa: ( 1), (
1), ( 2),…,(
2),…,(
 ). Wir wissen jetzt, dass es bei beliebigem x
stets eines von unseren
). Wir wissen jetzt, dass es bei beliebigem x
stets eines von unseren  i gibt, sowie eine Einheit
i gibt, sowie eine Einheit  , derart dass für
, derart dass für  = x
= x
 i die
Ungleichungen (2) bestehen.
i die
Ungleichungen (2) bestehen.
Es sei  =
=  1
1 1 +
1 +  2
2 2 + … +
2 + … +  n
n n und
n und 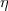 =
= 
 i-1 = x
i-1 = x . Bei dieser
Multiplikation mit
. Bei dieser
Multiplikation mit  i-1 (einer gewissen unserer
i-1 (einer gewissen unserer  festen Zahlen
festen Zahlen  1,…,
1,…,
 ) werden
die
) werden
die  i durch passende Linearkombinationen
i durch passende Linearkombinationen 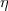 i ersetzt. Da nur endlich viele
i ersetzt. Da nur endlich viele  i in
Frage kommen, sind die Koeffizienten dieser Linearkombinationen beschränkt und
da |
i in
Frage kommen, sind die Koeffizienten dieser Linearkombinationen beschränkt und
da | i|<
i|<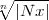 ist, folgt für die
ist, folgt für die 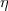 i wenigstens eine Abschätzung der Form
|
i wenigstens eine Abschätzung der Form
|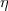 i|< D .
i|< D .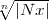 , wo D eine absolute Konstante ist:
, wo D eine absolute Konstante ist:
Satz 1 Es gibt eine nur von k abhängige Konstante D von der Art, dass es zu
jeder Zahl x mit Nx≠0 eine Einheit  gibt, so dass,
gibt, so dass, 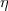 = x
= x =
= 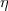 1
1 1 + … +
1 + … + 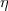 n
n n
gesetzt, gilt
n
gesetzt, gilt
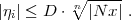
Sie sehen auch, dass dieser Satz wörtlich für Schiefkörper gilt.
Aus ihm ergeben sich nun leicht im Falle eines Zahlkörpers die üblichen Existenzsätze über Einheiten.
Man denke sich nämlich die Körper in der üblichen Weise angeordnet: Erst r1 reelle, dann r2 komplexe, dann die dazu konjugiert komplexen. Man bilde
(3)
x(1) =  1(1)x1 + 1(1)x1 +  2(1)x2 + … + 2(1)x2 + … +  n(1)xn n(1)xn |
x(2) =  1(2)x1 + 1(2)x1 +  2(2)x2 + … + 2(2)x2 + … +  n(2)xn n(2)xn |
..................................... . |
x(n) =  1(n)x1 + 1(n)x1 +  2(n)x2 + … + 2(n)x2 + … +  n(n)xn n(n)xn |
Dabei denke man sich x(1),… als wirkliche Zahlen und nicht mehr als hyperkomplexe. Das ist ja übrigens damit gleichwertig, wenn unter x immer gleich das System der Konjugierten verstanden wird. Die linken Seiten in (3) dürfen beliebig reell vorgeschrieben werden, wenn nur für konjugiert komplexe Konjugierte dieselbe reelle Zahl genommen wird. Dies gibt für die linken Seiten r + 1 Möglichkeiten (r = r1 + r2 - 1).
Man wähle nun r dieser r + 1 Zahlen „enorm gross“ und bestimme die
(r + 1)-te so, dass |Nx| = |x(1)|…|x(n)| = 1 wird. Zu diesem x gibt es eine Einheit
 , so dass die Koordinaten von x
, so dass die Koordinaten von x absolut kleiner D sind (|Nx| = 1). Wenn nun
die Koordinaten von x
absolut kleiner D sind (|Nx| = 1). Wenn nun
die Koordinaten von x beschränkt sind, so haben die Konjugierten x(i)
beschränkt sind, so haben die Konjugierten x(i) (i) auch
„bescheidene“ Werte, da sie nur Linearformen der Koordinaten sind. Folglich
muss
(i) auch
„bescheidene“ Werte, da sie nur Linearformen der Koordinaten sind. Folglich
muss  (i) auf diejenigen Konjugierten x(i) verkleinernd gewirkt haben, die „enorm
gross“ gewählt wurden. Für diese muss |
(i) auf diejenigen Konjugierten x(i) verkleinernd gewirkt haben, die „enorm
gross“ gewählt wurden. Für diese muss | (i)| < 1 sein. Die restliche (oder beide
restlichen – falls konjugiert imaginär) Konjugierte |
(i)| < 1 sein. Die restliche (oder beide
restlichen – falls konjugiert imaginär) Konjugierte | (i)| muss jetzt > 1 sein, damit
|N
(i)| muss jetzt > 1 sein, damit
|N | = 1 ist. Diese restliche kann unter den ersten r + 1 beliebig ausgewählt
werden:
| = 1 ist. Diese restliche kann unter den ersten r + 1 beliebig ausgewählt
werden:
Satz 2. Bei beliebig gegebenem i zwischen 1 und r + 1 gibt es eine Einheit  i
für die gilt:
i
für die gilt:
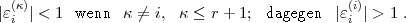
 1,
1, 2,…,
2,…, r+1. Von diesen behalte man nur die ersten
r.
r+1. Von diesen behalte man nur die ersten
r.
Ist  eine beliebige Einheit, so setze man
eine beliebige Einheit, so setze man
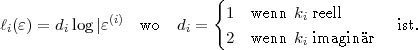 |
Dabei sei 1 < i < r+1. Kennt man die Logarithmen, so kennt man auch | (i)| und zwar für
alle i < r.151
Haben Einheiten gleiche Logarithmen, so hat ihr Quotient die Logarithmen Null.
Dann ist |
(i)| und zwar für
alle i < r.151
Haben Einheiten gleiche Logarithmen, so hat ihr Quotient die Logarithmen Null.
Dann ist | (i)| = 1, also
(i)| = 1, also  eine Einheitswurzel, was wie üblich leicht bewiesen
wird.
eine Einheitswurzel, was wie üblich leicht bewiesen
wird.
Durch Angabe der Log[arithmen] ist also eine Einheit bis auf Einheitswurzeln
bestimmt. Es genügt aber wegen 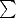 i=1r+1
i=1r+1 i(
i( ) = log |N
) = log |N | = log 1 = 0, die ersten
r Logarithmen zu kennen.
| = log 1 = 0, die ersten
r Logarithmen zu kennen.
Man nehme nun einen r-dimensionalen Raum und ordne jeder Einheit  zu
den Vektor mit den Komponenten xi =
zu
den Vektor mit den Komponenten xi =  i(
i( ). Diese Vektoren bilden eine additive
Gruppe. Beschränkte xi bedeuten beschränkte Logarithmen (auch der r + 1-te
wegen der Relation) also beschränkte Beträge der Konjugierten. Da es
ganze Körperzahlen sind, tun dies nur endlich viele. In einem endlichen
Volumteil liegen somit nur endlich viele. Also bilden unsere Vektoren einen
Vektormodul ohne Häufungspunkte, also ein Gitter. Bleibt zu zeigen,
dass es r-dimensional ist, dass es also r linear unabhängige Vektoren
gibt. Das tun nun die
). Diese Vektoren bilden eine additive
Gruppe. Beschränkte xi bedeuten beschränkte Logarithmen (auch der r + 1-te
wegen der Relation) also beschränkte Beträge der Konjugierten. Da es
ganze Körperzahlen sind, tun dies nur endlich viele. In einem endlichen
Volumteil liegen somit nur endlich viele. Also bilden unsere Vektoren einen
Vektormodul ohne Häufungspunkte, also ein Gitter. Bleibt zu zeigen,
dass es r-dimensional ist, dass es also r linear unabhängige Vektoren
gibt. Das tun nun die  1,
1, 2,…,
2,…, r. Denn es ist
r. Denn es ist  i(
i(
 ) < 0 für i≠
) < 0 für i≠ dagegen
dagegen
 i(
i( i) > 0.
i) > 0.
Ferner ist 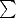
 =1r
=1r
 (
( i) = log |N
i) = log |N |-
|-  r+1(
r+1( i) = -
i) = - r+1(
r+1( i) > 0, da wegen
i≠r + 1 stets
i) > 0, da wegen
i≠r + 1 stets  r+1(
r+1( i) < 0 ist. Hilfssatz zeigt jetzt |
i) < 0 ist. Hilfssatz zeigt jetzt | i(
i(
 )|≠0.
)|≠0.
q.e.d.
Das ist doch alles ganz gut zu verstehen und, wie mir scheint, besser als mit den bisherigen Beweisen. Sie überlegen sich leicht, wie man im Kolleg die Klippe mit hyperkomplex umgeht, was nicht schwer ist.
Natürlich ist auch klar, dass prinzipiell auch im letzten Teil keine Logarithmen erforderlich sind, doch wäre eine Vermeidung nur gekünstelt und wenigstens bei diesem Beweis nicht am Platze.
Satz 1 ist meines Erachtens nach bereits die wesentliche Existenzaussage. Dass bei den Zahlkörpern ihre genauere Struktur noch hinzu kommen muss um zu den üblichen Sätzen zu gelangen ist ja selbstverständlich.
Kommentare zum Brief Nr.17:
Artin antwortet in diesem Brief auf drei Sendungen von Hasse. Und zwar: