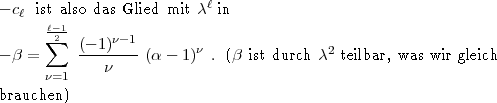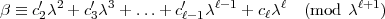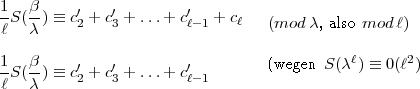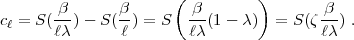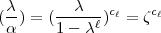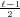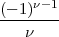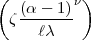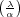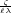4 Datum unbekannt, Brief von Artin an Hasse
Zum II Ergänzungssatz VII.
Lieber Herr Hasse!
Zunächst meinen besten Dank für Ihren Brief. Selbstverständlich ist Ihre
Herleitung einfacher. Ich bin aber unterdessen zu einer allgemeinen Formel für
jedes semiprimäre  gelangt, wenn also
gelangt, wenn also 
 1 (mod
1 (mod  2) (also ebensogut
2) (also ebensogut  rat[ionale] Zahl (
rat[ionale] Zahl ( 2).) Damit ist im Kreiskörper der Ergänzungssatz erledigt, da
dort jede Zahl durch Multiplikation mit einer Einheitswurzel semiprimär wird.
Die Formel bezieht sich aber nicht auf den Zähler
2).) Damit ist im Kreiskörper der Ergänzungssatz erledigt, da
dort jede Zahl durch Multiplikation mit einer Einheitswurzel semiprimär wird.
Die Formel bezieht sich aber nicht auf den Zähler  , sondern auf den Zähler
, sondern auf den Zähler  . Sie
lautet: (Körper beliebig)
. Sie
lautet: (Körper beliebig)
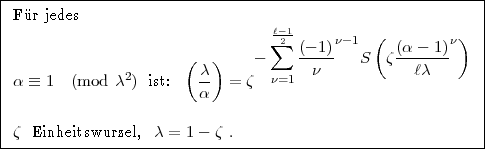 Beweis: Ich setze wie bei Ihnen: (Die Entwicklungsmöglichkeit ist leicht
einzusehen)
Beweis: Ich setze wie bei Ihnen: (Die Entwicklungsmöglichkeit ist leicht
einzusehen)
 Das Glied 1 -
Das Glied 1 -  kommt nicht vor, da
kommt nicht vor, da 
 1 (
1 ( 2).
2).
Man nehme beiderseits den Logarithmus und entwickle in Reihen. Wir suchen
rechts das Glied mit 
 . Die rechte Seite lautet:
. Die rechte Seite lautet:
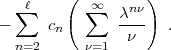 Da
n > 2 ist (hier wird wieder das semiprimär gebraucht) kommen, weil
Da
n > 2 ist (hier wird wieder das semiprimär gebraucht) kommen, weil  Primzahl
ist, für n≠
Primzahl
ist, für n≠ nur die Glieder
nur die Glieder 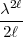 ,
, 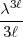 ,… in Frage. Sie enthalten aber ersichtlich
höhere Potenzen von
,… in Frage. Sie enthalten aber ersichtlich
höhere Potenzen von  . Bleibt also nur n =
. Bleibt also nur n =  ,
,  = 1. Der Koeffizient rechts von
= 1. Der Koeffizient rechts von

 ist also -c
ist also -c . Die linke Seite sieht so aus:
. Die linke Seite sieht so aus:
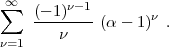
Für das Glied mit 
 kommen aber, da
kommen aber, da  - 1 durch
- 1 durch  2 teilbar ist, nur die Glieder
bis
2 teilbar ist, nur die Glieder
bis  =
= 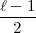 in Frage. (Auch
in Frage. (Auch  =
=  ist nicht notwendig trotz des Nenners.)
ist nicht notwendig trotz des Nenners.)
Sei nun:
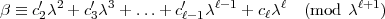 Dann ist:
Dann ist:
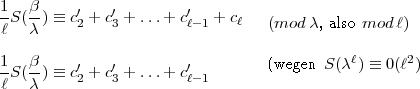
[Randnotiz von Artin:] Ich mache langsam Fortschritte in  -adik. Nun logarithmiere ich
schon!
-adik. Nun logarithmiere ich
schon!
Also:
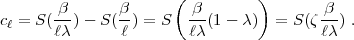 Nun ist wie Sie wissen:
Nun ist wie Sie wissen:
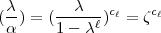
Also:
( ) =
) =  -
-
 =1
=1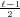
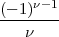 S
S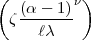
[Randnotiz von Artin:] Als  -adiker können Sie schreiben:
-adiker können Sie schreiben: 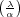 =
=  -S(
-S(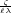 log
log  )
)
für 
 1 (mod
1 (mod  2). Hoffentlich ist nicht wieder ein Rechenfehler passiert, es ist sehr
heiss!
2). Hoffentlich ist nicht wieder ein Rechenfehler passiert, es ist sehr
heiss!
Daraus in bekannter Weise in beliebigen Körpern.
Dass Potenzen eine Rolle spielen ist kein Wunder, siehe  = 2.
= 2.
Diese Formel scheint mir die endgültige zu sein. Hoffentlich gelingt etwas
ähnliches beim allgemeinen Reziprozitätsgesetz.
Ich kann bis Dienstag bleiben, werde also, wenn Sie mich so lange bei
Ihnen dulden, etwa Montag abend wegfahren. Ich freu mich schon sehr
darauf wieder mal mit Ihnen beisammen zu sein. Hoffentlich ist das Wetter
gut.
Mit herzlichen Grüssen an alle Bekannten
Ihr
E. Artin
 gelangt, wenn also
gelangt, wenn also 
 1 (mod
1 (mod  2) (also ebensogut
2) (also ebensogut  rat[ionale] Zahl (
rat[ionale] Zahl ( 2).) Damit ist im Kreiskörper der Ergänzungssatz erledigt, da
dort jede Zahl durch Multiplikation mit einer Einheitswurzel semiprimär wird.
Die Formel bezieht sich aber nicht auf den Zähler
2).) Damit ist im Kreiskörper der Ergänzungssatz erledigt, da
dort jede Zahl durch Multiplikation mit einer Einheitswurzel semiprimär wird.
Die Formel bezieht sich aber nicht auf den Zähler  , sondern auf den Zähler
, sondern auf den Zähler  . Sie
lautet: (Körper beliebig)
. Sie
lautet: (Körper beliebig)
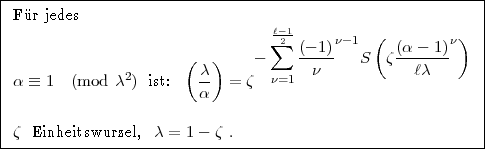


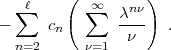
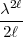
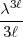

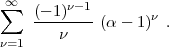
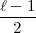 in Frage. (Auch
in Frage. (Auch