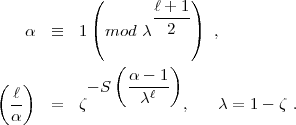
Lieber Herr Hasse!
Hoffentlich ist diese dritte Mitteilung die letzte! Ich möchte Ihnen aber noch eine Formel mitteilen die wohl die wahre ist:
In jedem Körper gilt für:
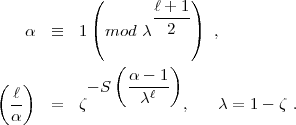
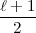 herabgedrückt.
herabgedrückt.
Es genügt, wie aus meinem Brief folgt, die Formel für den Kreiskörper zu beweisen.

 ) =
) =  für 1 <
für 1 <  <
<  - 1 wie Sie leicht nachrechnen.
- 1 wie Sie leicht nachrechnen.
 =
= 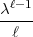 , so ist
, so ist  eine Einheit. Nun genügt
eine Einheit. Nun genügt  der
Gleichung (
der
Gleichung ( -1)
-1) +1 = 0. Ausgerechnet und durch
+1 = 0. Ausgerechnet und durch 
 dividiert findet
man:
dividiert findet
man:
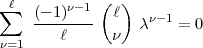
 <
<  - 1 ist nun
- 1 ist nun 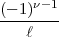 (
(

 )
)

 (mod
(mod  ). Dies gibt:
). Dies gibt:
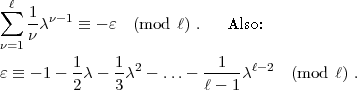
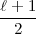 . Dann ist
. Dann ist 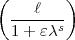 =
=  -1 (s <
-1 (s <  ).
).
Beweis:
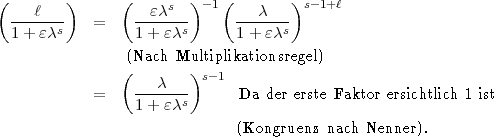
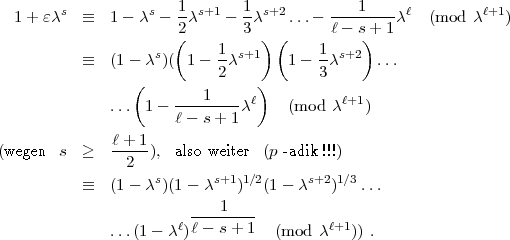
 gilt
gilt 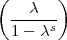 s =
s = 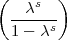 = 1, also
= 1, also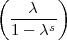 = 1:
= 1:
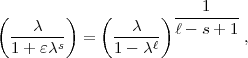
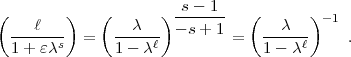
 setzen und
erhalten nach Ihrer Formel:
setzen und
erhalten nach Ihrer Formel:
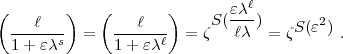
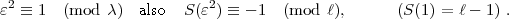
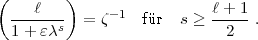

 1(
1(
 ) :
) :  = 1 +
= 1 + 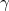

 . Dann ist wie sie sofort bestätigen
. Dann ist wie sie sofort bestätigen
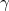
 -S
-S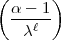 (mod
(mod  ), also:
), also: 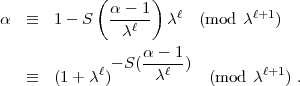
Nach Ihrer Formel etwa und wegen I folgt:
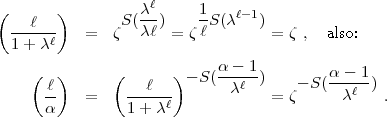
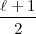 , s <
, s <  - 1. Es sei bewiesen, dass für
- 1. Es sei bewiesen, dass für 
 1 (mod
1 (mod  s+1) gilt
s+1) gilt
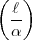 =
=  -S(
-S(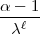 )
. (Dies ist der Fall für s =
)
. (Dies ist der Fall für s =  - 1 wegen IV. Daher
Induktion.)
- 1 wegen IV. Daher
Induktion.)
Nun sei 
 1 (mod
1 (mod  s)),
s)),  = 1 +
= 1 + 
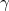
 s, wo
s, wo  unsere Einheit ist. Es
ist:
unsere Einheit ist. Es
ist:
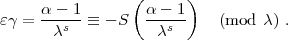

 -1 (mod
-1 (mod  ) ,
) , 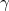
 S
S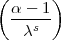 . Also:
. Also:
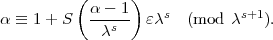
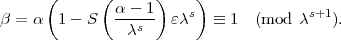
 =
=  -
-  S
S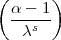

 s
s 
 - S
- S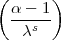

 s (mod
s (mod 
 +1),
(wegen s >
+1),
(wegen s >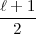 ). Also haben wir:
). Also haben wir:
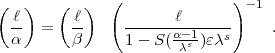
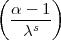

 s
s  (1 +
(1 + 
 s)-S(
s)-S(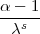 )
(mod
)
(mod 
 +1) , (wegen
s >
+1) , (wegen
s >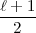 ) also
) also
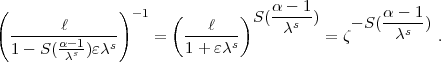
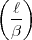 =
= 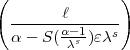 . Also wegen
. Also wegen 
 1 (
1 ( s+1) nach
Voraussetzung
s+1) nach
Voraussetzung
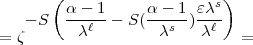
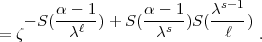
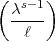 =
=  S(
S( s-1) = 1, also:
s-1) = 1, also:
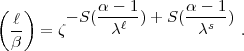
a.) b.) geben zusammen:
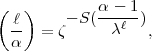

 1 (
1 ( s). Damit ist alles bewiesen. Die Formel enthält alle
vorigen Fälle, wie Sie leicht sehen können.
s). Damit ist alles bewiesen. Die Formel enthält alle
vorigen Fälle, wie Sie leicht sehen können.
Recht herzliche Grüsse
Ihr Artin
N.B. Das Rekurieren auf die frühere Formel lässt sich natürlich
auch vermeiden. Ebenso ist der Exponent ganz nach dem Satze von
Landsberg.12
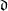 =
= 
 -2.
-2.