 zyklotomisch ist. Hierauf
wurden wir durch die folgende Mitteilung von Patterson aufmerksam
gemacht:31
zyklotomisch ist. Hierauf
wurden wir durch die folgende Mitteilung von Patterson aufmerksam
gemacht:31
Das missing link zu seinem Beweis fand Artin nach eigenem Bekunden in der Arbeit [Che26] von Tschebotareff, die 1925/26 erschienen war. Dies hatte er ja schon in seinem Brief Nr.6 vom 10.2.1926 vermutet, und er hatte das bestätigt im Brief Nr.8, allerdings ohne das weiter zu erläutern. Im vorliegenden Brief Nr.9 aber, wo Artin in der Beilage seinen Beweis im Detail ausführt, wird es deutlich, was er meint. Artin benutzt nicht etwa den Dichtigkeitssatz, den Tschebotareff in seiner Arbeit bewiesen hatte, sondern es geht nur um die Methode, die Tschebotareff zum Beweis seines Dichtigkeitssatzes verwendet hatte, und die in geeigneter Abänderung auch in der Artinschen Arbeit zur Anwendung kommt.
Es handelt sich um die heute so genannte „Durchkreuzungsmethode“. Das heute übliche Wort „durchkreuzen“ findet sich in diesem Zusammenhang in Teil II des Hasseschen Klassenkörperberichts [Has30a]. Artin selbst benutzt im Brief und in seiner Arbeit das Wort „überschneiden“.
Diese Methode beruht darauf, dass erstens sich das allgemeine Reziprozitätsgesetz für eine zyklotomische Erweiterung einfach und schnell verifizieren lässt. Wir hatten ja schon in 5.6 auf Seite 139 erwähnt, dass das Artinsche Reziprozitätsgesetz für zyklotomische Erweiterungen zum klassischen Bestandteil der algebraischen Zahlentheorie gehört. Zweitens wird eine gegebene abelsche Erweiterung K|k mit einer geeigneten, zu K|k linear disjunkten zyklotomischen Erweiterung K'|k verglichen. Die Galoisgruppe des Kompositums KK' ist das direkte Produkt der Galoisgruppe von K|k mit der von K'|k. Aufgrund der funktoriellen Eigenschaften der Frobenius-Substitution gelingt es dann, von K'|k auf K|k zu schliessen.
Mit anderen Worten: Die „Durchkreuzung“ besteht in der Übertragung von Eigenschaften des (geeignet zu wählenden) zyklotomischen Körpers K'|k auf den gegebenen abelschen Körper K|k.
Das ist in der Tat eine bemerkenswerte Methode. Stevenhagen und Lenstra bemerken dazu in ihrem Artikel [SL96]:
Chebotarev’s technique is still a crucial ingredient of all known proofs of Artins Reciprocity Law.
Das ist richtig. Wenn die Autoren aber weiter schreiben:
It is widely felt that it works for no good reason …
dann ist uns nicht recht klar, was mit der letzteren Bemerkung gemeint ist. Durch die Methode von Tschebotareff wird ja in Evidenz gesetzt, dass die Gesetze der Klassenkörpertheorie im Grunde auf die Gesetze in zyklotomischen Körpern zurückgehen. Und das erscheint uns durchaus als ein good reason. Aber vielleicht kommt das in der von Artin verwendeten Version nicht so klar zum Ausdruck wie in der späteren Version von Hasse aus dem Jahre 1932 in [Has33a]. Dort beweist Hasse das Artinsche Reziprozitätsgesetz mit Hilfe der Algebrentheorie, und die „Methode von Tschebotareff“ erscheint als der Satz, dass jede Divisionsalgebra bereits durch geeignete zyklotomische Körper zerfällt wird.
Übrigens ist die Durchkreuzungsmethode schon früher, lange vor Tschebotareff,
angewandt worden, nämlich 1896 durch Hilbert bei seinem Beweis des Satzes von
Kronecker-Weber, dass jede abelsche Erweiterung von  zyklotomisch ist. Hierauf
wurden wir durch die folgende Mitteilung von Patterson aufmerksam
gemacht:31
zyklotomisch ist. Hierauf
wurden wir durch die folgende Mitteilung von Patterson aufmerksam
gemacht:31
Eine Bemerkung zu dem Satz von Tschebotareff. Was ganz kurios
dabei ist, ist, dass die Techniken alle schon 1896 zur Verfügung
standen. Tsch[ebotareff ] verbindet die Ideen von Frobenius mit
der Methode, die Hilbert entwickelt hat, um den Kronecker-Weber
Satz zu beweisen. Beide Arbeiten sind 1896 erschienen. Beim
Beweis geht es um die Untersuchung der Eigenschaften von
K 

 (
(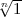 ); seit 1885 hat man den Satz von Dedekind, dass
dieser Ring eine Summe von Körpern ist (Artinsche Ringe!) …
); seit 1885 hat man den Satz von Dedekind, dass
dieser Ring eine Summe von Körpern ist (Artinsche Ringe!) …
Hilbert vergleicht einen gegebenen abelschen Körper K| (den man als
zyklischen Körper von Primzahlpotenzgrad annehmen kann) mit geeignet
konstruierten zyklotomischen Körpern Z. Die Konstruktion dieser zyklotomischen
Körper ist derart, dass man aus dem Vergleich des Verzweigungsverhaltens der
Primzahlen in K und in Z schließen kann, dass K schon selbst ein zyklotomischer
Körper ist. Allerdings kommen bei Hilbert keine Frobenius-Automorphismen
vor.
(den man als
zyklischen Körper von Primzahlpotenzgrad annehmen kann) mit geeignet
konstruierten zyklotomischen Körpern Z. Die Konstruktion dieser zyklotomischen
Körper ist derart, dass man aus dem Vergleich des Verzweigungsverhaltens der
Primzahlen in K und in Z schließen kann, dass K schon selbst ein zyklotomischer
Körper ist. Allerdings kommen bei Hilbert keine Frobenius-Automorphismen
vor.
Artin kannte natürlich sowohl die Arbeit von Frobenius als auch den Beweis von Hilbert. Im Grunde hätte er also schon 1923, in seiner L-Reihenarbeit, durch Verbindung der Ideen von Frobenius und von Hilbert einen Beweis seines Reziprozitätsgesetzes geben können; er hätte nicht auf Tschebotareff zu warten brauchen. Aber wie oft in solchen Fällen fehlte damals wohl der entscheidende Anstoß. Jetzt, im Jahre 1927, war offenbar die Zeit reif, sodass der durch die Arbeit von Tschebotareff erfolgte Anstoß von Artin aufgenommen und umgesetzt werden konnte.