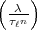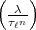7.1 Die Methode von Eisenstein.
In diesem Brief geht es um den zweiten Ergänzungssatz zum Reziprozitätsgesetz
für das Potenzrestsymbol, und zwar zum Exponenten  n, wobei
n, wobei  eine (ungerade)
Primzahl ist; es wird im Körper der
eine (ungerade)
Primzahl ist; es wird im Körper der  n-ten Einheitswurzeln gerechnet. In
den früheren Briefen aus dem Jahre 1923 ging es um den Fall n = 1.
Die damals von Artin und Hasse gewonnenen Resultate fanden ihren
Niederschlag in einer gemeinsamen Arbeit [AH25] aus dem Jahre 1925.
Nun soll der Fall n > 1 behandelt werden, und zwar zunächst offenbar
n = 2.
n-ten Einheitswurzeln gerechnet. In
den früheren Briefen aus dem Jahre 1923 ging es um den Fall n = 1.
Die damals von Artin und Hasse gewonnenen Resultate fanden ihren
Niederschlag in einer gemeinsamen Arbeit [AH25] aus dem Jahre 1925.
Nun soll der Fall n > 1 behandelt werden, und zwar zunächst offenbar
n = 2.
Wir wissen nicht, welches der von Hasse vorgeschlagene Weg gewesen ist, den
Artin erwähnt und der offenbar nicht zum Ziel geführt hat. Die neue, jetzt
von Artin vorgeschlagene Methode ist einer alten Arbeit von Eisenstein
entnommen. Artin spricht von „der bekannten Crelle-Arbeit“ von Eisenstein.
Nun hatte Eisenstein 37 Arbeiten im Crelleschen Journal. Gemeint ist
offenbar die Arbeit [Eis50b] aus dem Jahre 1850, erschienen in Band 39,
mit dem Titel: „Über ein einfaches Mittel zur Auffindung der höheren
Reciprocitätsgesetze und der mit ihnen zu verbindenden Ergänzungssätze“. Diese
Arbeit wurde schon in der gemeinsamen Note [AH25] von Artin und Hasse zum
zweiten Ergänzungssatz bei Primzahlexponenten m =  zitiert. Deshalb
konnte Artin in seinem Brief getrost auf „die bekannte Crelle-Arbeit von
Eisenstein“ hinweisen. Er hatte ja Hasse schon vor dem 30.Juni 1923,
wahrscheinlich aber schon im März 1923 anlässlich von Hasses Vortrag in
Hamburg darauf hingewiesen. Das Artinsche Umdrehverfahren, das wir in 5.3
beschrieben haben, war ebenfalls im wesentlichen aus der Eisensteinschen Arbeit
extrahiert.
zitiert. Deshalb
konnte Artin in seinem Brief getrost auf „die bekannte Crelle-Arbeit von
Eisenstein“ hinweisen. Er hatte ja Hasse schon vor dem 30.Juni 1923,
wahrscheinlich aber schon im März 1923 anlässlich von Hasses Vortrag in
Hamburg darauf hingewiesen. Das Artinsche Umdrehverfahren, das wir in 5.3
beschrieben haben, war ebenfalls im wesentlichen aus der Eisensteinschen Arbeit
extrahiert.
Dass Artin ausdrücklich von der „Crelle“-Arbeit spricht, hat seinen Grund
wahrscheinlich darin, dass Eisenstein im selben Jahr 1850 eine zweite, ebenfalls
fundamentale Arbeit über das Reziprozitätsgesetz publizierte, die jedoch nicht im
Crelleschen Journal erschien, sondern in den Berliner Akademieberichten
[Eis50a].
Eisenstein hatte in seiner Arbeit gezeigt, wie man im Kreiskörper
explizite Formeln für das Reziprozitätsgesetz „durch eine eigentümliche
Induktion“, wie er sagt, auffinden kann – wenn man nur annimmt, dass
das Reziprozitätsgesetz gewisse Grundeigenschaften besitzt. Eisenstein
behandelt nur den Fall des Körpers der  -ten Einheitswurzeln, wobei
-ten Einheitswurzeln, wobei  eine
ungerade Primzahl ist, aber er sagt deutlich, dass dies zwar nicht der
allgemeinste Fall ist, aber doch ein „Fall von großer Allgemeinheit, aus dem die
unbeschränkte Anwendbarkeit des Verfahrens erhellen wird“. Das lässt wohl darauf
schließen, dass er dieses Verfahren auch für den Körper der
eine
ungerade Primzahl ist, aber er sagt deutlich, dass dies zwar nicht der
allgemeinste Fall ist, aber doch ein „Fall von großer Allgemeinheit, aus dem die
unbeschränkte Anwendbarkeit des Verfahrens erhellen wird“. Das lässt wohl darauf
schließen, dass er dieses Verfahren auch für den Körper der  (
( n) der
n) der  n-ten
Einheitswurzeln für beliebiges n konzipiert hatte. (Dabei bedeutet
n-ten
Einheitswurzeln für beliebiges n konzipiert hatte. (Dabei bedeutet  n eine
primitive
n eine
primitive  n-te Einheitswurzel.) Artin führt das nunmehr für den Fall
n-te Einheitswurzel.) Artin führt das nunmehr für den Fall  2
durch.
2
durch.
Zum Umkehrfaktor 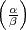
 -1 siehe Seite 60. Er ist zunächst nur dann
definiert, wenn
-1 siehe Seite 60. Er ist zunächst nur dann
definiert, wenn  ,
, zueinander und zu
zueinander und zu  prim sind. Aber schon Eisenstein
bemerkt, dass man die Definition auf beliebige
prim sind. Aber schon Eisenstein
bemerkt, dass man die Definition auf beliebige  ,
, ≠0 ausdehnen kann, nach
folgendem Prinzip:
≠0 ausdehnen kann, nach
folgendem Prinzip:
Es sei  = 1-
= 1- gesetzt.
gesetzt.
 ist eine Primzahl, und zwar für den einzigen Primdivisor
ist eine Primzahl, und zwar für den einzigen Primdivisor  von
von  (
( ), der über der
Primzahl
), der über der
Primzahl  liegt. Als Grundannahme setzt Eisenstein voraus, dass der Umkehrfaktor
in der Form
liegt. Als Grundannahme setzt Eisenstein voraus, dass der Umkehrfaktor
in der Form  L angesetzt werden kann, wobei L = f(
L angesetzt werden kann, wobei L = f( ,
, ), wie wir heute sagen
würden, eine im
), wie wir heute sagen
würden, eine im  -adischen Sinne stetige Funktion von
-adischen Sinne stetige Funktion von  ,
, ist, mit Werten in
ist, mit Werten in
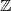 /
/ n.
Demnach kann der Umkehrfaktor auch dann wohldefiniert werden, wenn
n.
Demnach kann der Umkehrfaktor auch dann wohldefiniert werden, wenn  ,
, nicht zueinander prim sind; in diesem Falle ersetze man
nicht zueinander prim sind; in diesem Falle ersetze man  ,
, durch hinreichend
benachbarte
durch hinreichend
benachbarte  ',
', ' aus
' aus  (
( ), die zueinander prim sind.
), die zueinander prim sind.
Heute würden wir  L als das Hilbertsche Symbol
L als das Hilbertsche Symbol 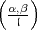 ansetzen, definiert für
beliebige
ansetzen, definiert für
beliebige  ,
, aus der
aus der  -adischen Komplettierung
-adischen Komplettierung 
 (
( ). Siehe dazu Seite
60.
). Siehe dazu Seite
60.
Die von Artin definierten Elemente  a = 1 -
a = 1 - a erzeugen die Einseinheitengruppe
von
a erzeugen die Einseinheitengruppe
von 
 (
( ) als pro-endliche Gruppe. Das erklärt, weshalb Artin für den zweiten
Ergänzungssatz insbesondere auf die Symbole
) als pro-endliche Gruppe. Das erklärt, weshalb Artin für den zweiten
Ergänzungssatz insbesondere auf die Symbole 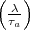 hinaus will. Für a /
hinaus will. Für a / 0 mod
0 mod  stellt sich heraus, dass
stellt sich heraus, dass 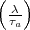 = 1. Deshalb steuert er sofort auf die Berechnung
von
= 1. Deshalb steuert er sofort auf die Berechnung
von 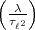 zu.
zu.
Artin bezeichnet den Umkehrfaktor von  a und
a und  b mit (a,b). Er ist nicht
direkt definiert, weil ja
b mit (a,b). Er ist nicht
direkt definiert, weil ja  a und
a und  b nicht teilerfremd sind, und daher muss auf die
obige Beschreibung als Hilbertsches Symbol zurückgegriffen werden. Das sagt
Artin allerdings nicht, weil er wohl annimmt, dass dies Hasse geläufig ist.
Eisenstein selbst gibt in [Eis50b] an, wie man (a,b) zu interpretieren hat: Man
ersetze
b nicht teilerfremd sind, und daher muss auf die
obige Beschreibung als Hilbertsches Symbol zurückgegriffen werden. Das sagt
Artin allerdings nicht, weil er wohl annimmt, dass dies Hasse geläufig ist.
Eisenstein selbst gibt in [Eis50b] an, wie man (a,b) zu interpretieren hat: Man
ersetze  a,
a, b durch zueinander prime Elemente der Form 1 - ka
b durch zueinander prime Elemente der Form 1 - ka a und
1 - kb
a und
1 - kb b wobei ka,kb
b wobei ka,kb  1 mod
1 mod  N mit hinreichend großem N zu wählen
sind.
N mit hinreichend großem N zu wählen
sind.
Diese Rechnungen in Artins Brief sind direkt den Eisensteinschen Rechnungen
nachvollzogen, nur jetzt eben für den Fall n = 2, was nur einen einzigen Schritt in
Eisensteins „eigentümlicher Induktion“ erforderlich macht. Wir wissen nicht,
weshalb Artin am Schluss nicht mehr explizit den errechneten Wert von 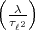 hinschreibt, nämlich
hinschreibt, nämlich  . Vielleicht nahm er an, dass Hasse dies schon für n = 2
wusste?
. Vielleicht nahm er an, dass Hasse dies schon für n = 2
wusste?
Anscheinend vermutete Artin, dass nicht nur für  2 sondern für eine beliebige
ungerade Primzahlpotenz
2 sondern für eine beliebige
ungerade Primzahlpotenz  n stets
n stets 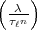 =
=  ist (und =
ist (und =  -1 für
-1 für  = 2). Denn ein
Jahr später, in seinem Brief Nr.17 vom 27.10.1927 spricht Artin davon, dass die
Hasseschen Rechnungen seine Vermutung
= 2). Denn ein
Jahr später, in seinem Brief Nr.17 vom 27.10.1927 spricht Artin davon, dass die
Hasseschen Rechnungen seine Vermutung 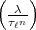 =
=  ±1 widerlegt haben.
Damals arbeiteten Artin und Hasse gemeinsam an ihrer zweiten Arbeit zum
Ergänzungssatz [AH28], die dann 1928 erschien.
±1 widerlegt haben.
Damals arbeiteten Artin und Hasse gemeinsam an ihrer zweiten Arbeit zum
Ergänzungssatz [AH28], die dann 1928 erschien.
 n, wobei
n, wobei  eine (ungerade)
Primzahl ist; es wird im Körper der
eine (ungerade)
Primzahl ist; es wird im Körper der  n-ten Einheitswurzeln gerechnet. In
den früheren Briefen aus dem Jahre 1923 ging es um den Fall n = 1.
Die damals von Artin und Hasse gewonnenen Resultate fanden ihren
Niederschlag in einer gemeinsamen Arbeit [AH25] aus dem Jahre 1925.
Nun soll der Fall n > 1 behandelt werden, und zwar zunächst offenbar
n = 2.
n-ten Einheitswurzeln gerechnet. In
den früheren Briefen aus dem Jahre 1923 ging es um den Fall n = 1.
Die damals von Artin und Hasse gewonnenen Resultate fanden ihren
Niederschlag in einer gemeinsamen Arbeit [AH25] aus dem Jahre 1925.
Nun soll der Fall n > 1 behandelt werden, und zwar zunächst offenbar
n = 2.


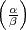

 ,
,


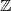
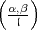 ansetzen, definiert für
beliebige
ansetzen, definiert für
beliebige 

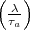 hinaus will. Für
hinaus will. Für 
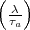
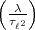 zu.
zu.
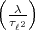 hinschreibt, nämlich
hinschreibt, nämlich