10.09.1926, Brief von Artin an Hasse

7 10.09.1926, Brief von Artin an Hasse

Hamburg, 10. Sept. 1926

Lieber Herr Hasse!

Vielen Dank für Ihren Brief. Den von Ihnen eingeschlagenen Weg habe ich (leider Gottes) in den Spezialfällen 2²,2³,3², angewendet. Für ² macht das aber zu viel Rechnung. Deshalb zog ich es vor, eine Methode von Eisenstein (die bekannte Crelle-Arbeit) zu verwenden:

Ich setze _a = 1 - _n^a. Dann gilt: _a+b - ^a_b = _a. Dies zieht die drei Kongruenzen:

_a+b ^a_b (mod_a); _a+b _a (mod_b); _a -^a_b (mod_a+b)

nach sich, so dass man findet:

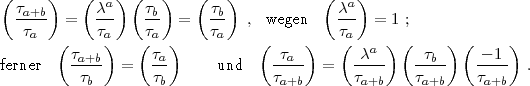
( ) ( a) ( ) ( ) ( a) ta+b = c-- tb = tb , wegen c-- = 1 ; ta ( t)a (ta ) ta ( ) t(a ) ( ) ( ) ta+b ta ta ca tb -1 ferner -t-- = t- und t--- = t--- t--- t--- . b b a+b a+b a+b a+b

Schreiben wir nun zur Abkürzung für den Umkehrfaktor:

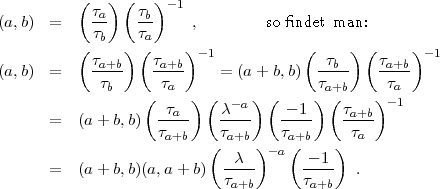
( ) ( ) ta tb - 1 (a,b) = tb ta , so findet man: ( ) ( )-1 ( ) ( ) -1 (a,b) = ta+b ta+b- = (a + b,b) -tb- ta+b tb ta ta+b ta ( t ) ( c- a) ( - 1 ) (t ) -1 = (a + b,b) --a- ---- ---- -a+b ta+b (ta+b ) ta+(b ) ta --c- -a ---1 = (a + b,b)(a,a + b) ta+b ta+b .

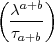= 1 ist, kann man auch schreiben:

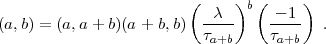
( )b ( ) (a,b) = (a,a+ b)(a+ b,b) -c-- --1- . ta+b ta+b

Sei

ungerade. Dann gilt einfacher:

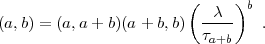
( )b (a,b) = (a,a + b)(a+ b,b) -c-- . ta+b

Sei nun n = 2. Man setze a = 1, b =

² - 1. Es wird:

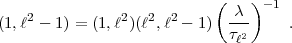
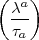( ) -1 2 2 2 2 c-- (1,l - 1) = (1,l )(l,l - 1) tl2 .

Nun ist

= 1 =

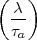^a .

Ist also a prim zu so wird ( )
c-
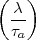ta = 1. Nun wende man die gleiche Formel an auf den einen Faktor:

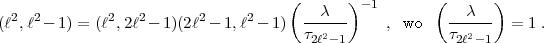
2 2 2 2 2 2 ( c )-1 ( c ) (l,l - 1) = (l ,2l -1)(2l - 1,l - 1) t-2--- , wo t--2-- = 1 . 2l- 1 2l- 1

_2²-1 = 1 -

^2²-1 wegen

^2²-1 =

₁

^-1 sicher primär ist, folgt
(

²,

² - 1) = 1. Also bleibt:

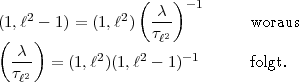
( c ) -1 (1,l2- 1) = (1,l2) --- woraus ( ) tl2 -c- = (1,l2)(1,l2- 1)-1 folgt. tl2

Nun ist:

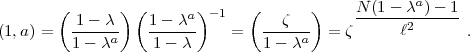
( ) ( a) -1 ( ) N-(1---ca)--1 (1,a) = 1---c- 1---c- = --z--- = z l2 . 1- ca 1- c 1- ca

Also:

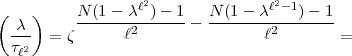
2 2 ( ) N-(1--cl-)--1- N-(1---cl--1)---1 c-- = z l2 - l2 = tl2

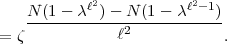
l2 l2-1 N-(1---c-)---N-(1---c----) = z l2 .

Hierin sind die Exponenten

^² bezw.

^²-1 hoch genug, um bei der Darstellung durch die symmetrischen Grundfunktionen dieser Potenzen beim 3-ten Glied abzubrechen. Drückt man die Grundfunktionen durch die Potenzsummen aus und lässt überflüssiges weg, so bleibt gerade der Anfang der gewünschten logarithmischen Entwicklung stehen von dem man sich auch überzeugt dass er ausreicht. Ich brauche das wohl nicht weiter auszuführen.

Ich komme also Dienstag und zwar mit dem Zug 13⁰² wie Sie vermutet haben. Bis dahin mit herzlichen Grüssen und einer Empfehlung an Frau Gemahlin

Ihr Artin

Kommentare zum Brief Nr.7:

7.1 Die Methode von Eisenstein.

[prev] [prev-tail] [front] [up]