About me
I am an "akademische Rätin auf Zeit" at Heidelberg University, a PI in the Research Station Geometry & Dynamics and in the Research training group "Asymptotic Invariants and Limits of Groups and Spaces", a member of the Young Researchers Convent in the cluster of excellence STRUCTURES, and involved in the founding of the Heidelberg Experimental Geometry Lab (HEGL).
In the winter term 2024/25, I was a guest professor at Saarland University and in Fall 2019, I was a Visiting Assistant Professor in Mathematics at NYU Shanghai. From April 2016 to August 2019, I was a Postdoctoral fellow at the University of Toronto, working with Kasra Rafi and Giulio Tiozzo. I did my PhD under the supervision of Gabriela Weitze-Schmithüsen. Furthermore, I am the senior editor of the Snapshots of modern mathematics from Oberwolfach.
I believe in the content of the statement of inclusiveness and the axioms set forth by Federico Ardila-Mantilla.
Infinite translation surfaces
Finite translation surfaces arise in very different contexts. There are relations to dynamical systems (in particular billiards), to Teichmüller theory, to geometric group theory, to algebraic geometry, and many other fields.
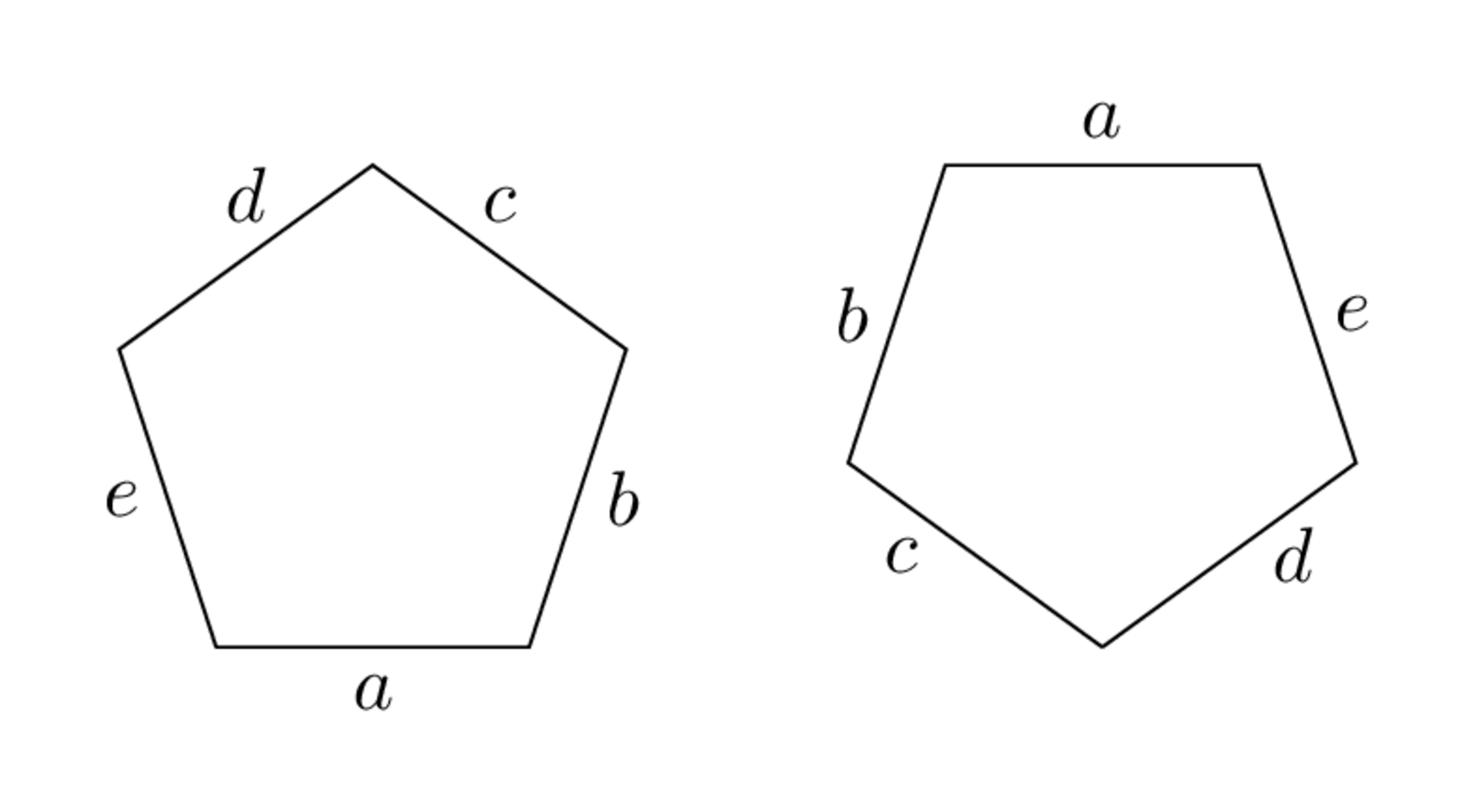 The most visual way to define a finite translation surface is by considering finitely many polygons in the plane. If every edge of the polygons can be identified with a parallel edge of the same length so that we obtain a connected, orientable surface then the resulting object is a translation surface.
In the picture, you can see a famous example which is called the double pentagon.
The most visual way to define a finite translation surface is by considering finitely many polygons in the plane. If every edge of the polygons can be identified with a parallel edge of the same length so that we obtain a connected, orientable surface then the resulting object is a translation surface.
In the picture, you can see a famous example which is called the double pentagon.
My research is concerned with a generalization of these objects, called infinite translation surfaces. They allow more variety compared to the finite case and in particular, the singularities can be more diverse. A common topological type that infinite translation surfaces have, is the one of a Loch Ness monster.
For more information on what I am interested in, see Research.
Teaching
In the summer term 2026, I offer a Proseminar with Anna Schilling on "Snapshots of modern mathematics". Please register in MÜSLI if you are interested in attending.
Since 2020, I taught the courses "(Big) mapping class groups", "Einführung in die Geometrie" (with Beatrice Pozzetti) and "Algebraic Topology I", held seminars (in particular in the Heidelberg Experimental Geometry Lab), and organized the exercise classes for Linear Algebra 1 and 2 as well as of a course on translation surfaces at Heidelberg University. In the winter term 2024/25, I taught Mathematics for computer scientists I at Saarland University. In fall 2019, I taught Honors Calculus at NYU Shanghai. Previously, I taught MATB43 (Introduction to Analysis), STAB41 (Financial Derivatives), and MATD01 (Fields and Groups) at University of Toronto Scarborough. For more information, see Teaching.