CP7 Lunch Seminar
This is the old webpage for the CP7 seminar. Please visit here for the current CP7 seminar website.
Purpose
The seminar is an informal meeting for members of CP7 and anyone who might be interested. Participants take turns at illustrating their area of research or a neighboring field, in 30-minute talks aimed at a broader audience. The goal is to stimulate discussions and explore possible collaborations at the interface between Mathematics and Physics.
Topics
The topics discussed are as broad as the topics of the members, comprising all the listed below and more.
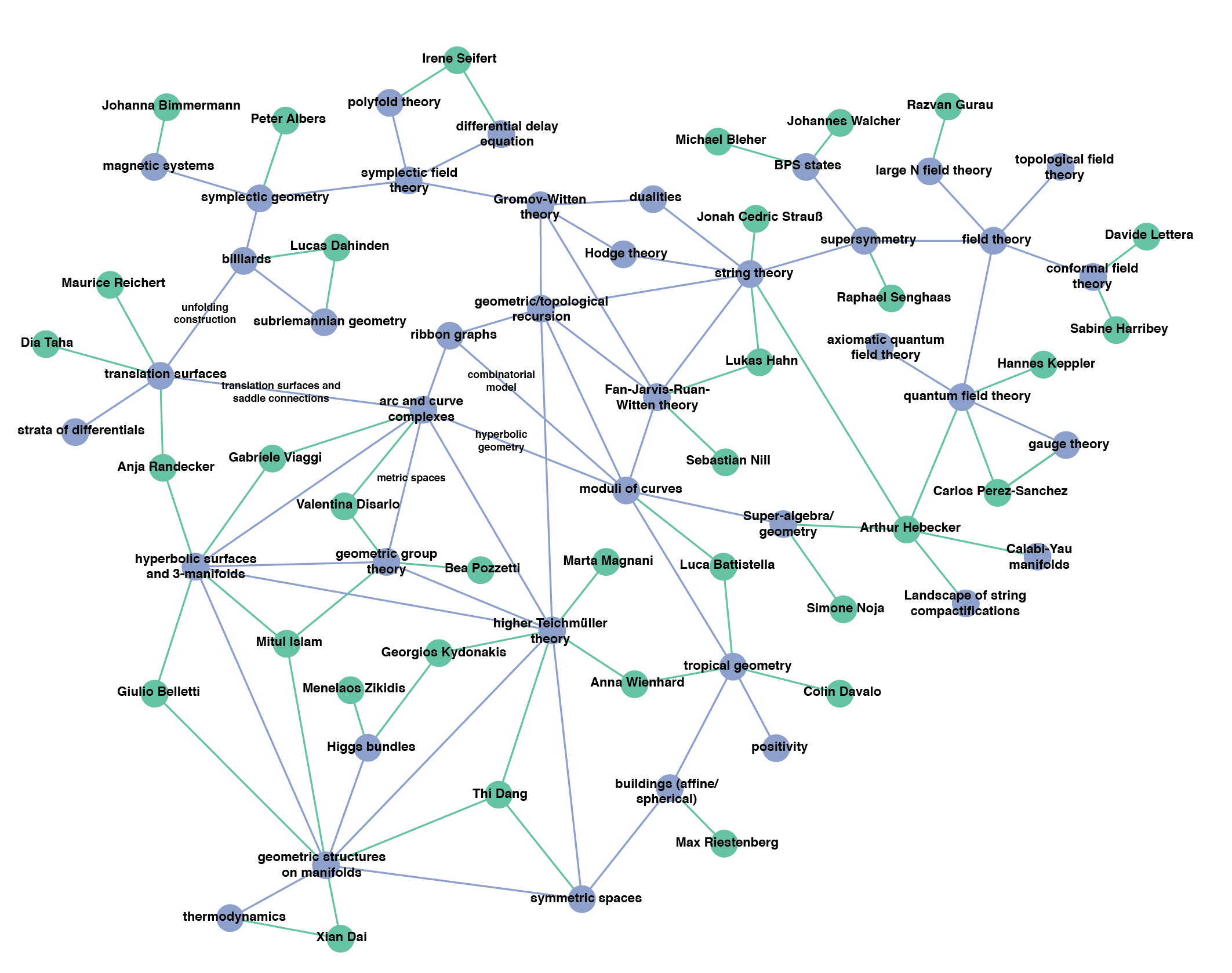If you are a member of CP7 and you are missing one of your topics, you are very welcome to send us any additional suggestions.
Time and date
The seminar is happening about every second week on Wednesday, 1-2pm, either hybrid in Seminarraum 8 in the Mathematikon or completely online. This is a lunch seminar, so the audience is welcome to have lunch during the seminar. For those in Seminarraum 8, we provide coffee. Please contact the organizers to receive the link to our meeting to participate remotely.
Summer semester 2022
| Date | Name | Title of talk |
|---|---|---|
| May 4 (hybrid) | Anja Randecker | Moduli spaces of differentials |
| Moduli problems and moduli spaces appear in physics in many different ways and for many different objects. Here, we want to approach one type of moduli spaces from the mathematical point of view. In the talk, I will introduce moduli spaces of (quadratic / abelian / holomorphic / meromorphic / ...) differentials and an action of GL(2,R) on it. I will also explain the objects in my favourite way: as polygons coming from (half-)translation structures on Riemann surfaces and their groups of symmetry. | ||
| May 11 (hybrid) | Oscar García-Prada | Kähler-Yang-Mills equations and gravitating vortices |
| I will start introducing the Kähler-Yang-Mills equations on a holomorphic vector bundle over a compact complex manifold. These equations, inspired by the Hitchin-Kobayashi correspondence for bundles and the Yau-Tian-Donaldson conjecture for constant scalar curvature Kähler metrics, intertwine the curvature of a Hermitian-Yang-Mills connection on the bundle and the scalar curvature of a Kähler metric on the manifold. After this, I will consider special symmetric solutions on a compact Riemann surface known as gravitating vortices. | ||
| May 25 (hybrid) | Gerben Venken | Trouble with getting the four spacetime dimensions of real life in string theory: an overview |
| Superstring theory in its most pedestrian formulation is a quantum gravity theory in 9+1 spacetime dimensions. To make contact with our real world with three spatial dimensions, six of the nine spatial dimensions should be compact and at a length scale smaller than that of our everyday life. Further, our effective 3+1 dimensional world at large length scales should have a positive vacuum energy to match cosmological observations. Despite decades of work, serious concerns still exist over whether a suitable controlled six-dimensional compact geometry exists which achieves these minimal conditions to make contact with our real world. In this talk, I will provide a biased overview of some of these concerns. | ||
| June 8 (hybrid) | Mengxue Yang | An introduction to opers |
| I would like to tell you a little bit about opers on a Riemann surface of genus at least 2. Since the definition of an oper using principal bundles is very abstract, I will give an intuitive explanation and then a more explicit description using vector bundles. Classical examples of opers can be related to familiar mathematical objects such as complex projective structures, jet bundles, and differential operators. Then I will discuss a recent generalization, (G,P)-opers, motivated by higher Teichmuller theory. Slides | ||
| June 29 (hybrid) | Sabine Harribey | Renormalization and tensor field theory |
| Quantum field theory is the extension of quantum mechanics to fields and describes the fundamental interactions in nature. These interactions are represented as perturbations of a Gaussian probability measure with a coupling parameter whose value indicates how far it is from being Gaussian. However, these objects are often ill-defined and when computing correlations many divergences arise. Renormalization was thus introduced in order to deal with these divergences. If the theory has a weak interaction, the coupling parameter is small and one can then perform very precise computations using a series development in this small coupling parameter. However, computations are much harder when the interaction is strong and the coupling parameter large. New methods thus need to be developed in order to find solvable strongly-coupled QFTs. In this talk, I will introduce the notions and ideas behind the renormalization group and explain how field theories based on random tensors can lead to analytical results for strongly-interacting models. | ||
| July 13 (hybrid) | Peter Smillie | Unstable minimal surfaces |
| I will present two techniques to construct unstable minimal surfaces in R^3, one using a certain flick of your wrist and the other using a bit of classical algebraic geometry. Then I will describe how this (specifically the second technique) lets you construct unstable minimal surfaces in some rank 3 symmetric spaces of non-compact type. | ||
| July 27 (online) | Discussion on topics and format for the seminar in fall | |
Winter semester 2021/22
| Date | Name | Title of talk |
|---|---|---|
| Oct 22, 4-5.30pm | Kickoff event (in person) with introductions and networking | |
| Nov 3 | Dominik Wrazidlo | Rational homotopy theory for singular spaces |
| Many spaces arising in topology and geometry are not manifolds, but have singularities, so that essential tools like classical Poincaré duality are no longer available. In this survey talk, I will present Banagl's method of intersection spaces that assigns rational Poincaré duality spaces to certain singular spaces by modifying only a neighborhood of the singular set. The homology of intersection spaces is not isomorphic to classical intersection homology of Goresky and MacPherson. However, both theories are known to be related by mirror symmetry on Calabi-Yau 3-folds. I will explain a new perspective on intersection space theory from the viewpoint of rational homotopy theory. The focus of this talk lies on a survey of main ideas, examples, and possible future directions of research. Slides | ||
| Nov 17 | Carlos Pérez | Dirac ensembles in noncommutative geometry: a gauge theory perspective |
| In high energy physics, one achievement of noncommutative geometry is the possibility to actually derive the observed particle spectrum (the Standard Model) from a simple input. This noncommutative geometrical description of matter works only at a classical level (and for the rest, the theory is 'patched' with ordinary quantum field theory methods). The main topic of this talk is a path-integral quantization approach that leads to the concept of 'random noncommutative geometry', i.e. ensembles of Dirac operators, the finite approximations of which can be restated as random multi-matrix ensembles with wildly non-factorizable measures and multi-trace interactions. After a friendly introduction to these topics, I will present a Dirac ensemble which can be identified with Yang-Mills-Higgs matrix theory. Slides | ||
| Dec 1 | Daniele Alessandrini | Spectral Networks and non-abelianization |
| I will give some ideas about the theory of Spectral Networks, developed by Gaiotto, Moore and Neitzke during their research on supersymmetric QFT. These objects have an independent interest for mathematicians, since they are related with holomorphic differentials on Riemann surfaces and with the geometry of character varieties. In the talk, I will explain how Spectral Networks can be used to define a non-abelianization map, and obtain some interesting coordinates on character varieties of surface groups that generalize the Fock-Goncharov coordinates. | ||
| Dec 15 | Alexandre Jannaud | Dehn-Seidel twist, C^0 symplectic geometry and barcodes |
| In this talk I will present my work initiating the study of the C^0 symplectic mapping class group, i.e. the group of isotopy classes of symplectic homeomorphisms, and present the proofs of the first results regarding the topology of the group of symplectic homeomorphisms. For that purpose, we will introduce a method coming from Floer theory and barcodes theory. Applying this strategy to the Dehn-Seidel twist, a symplectomorphism of particular interest when studying the symplectic mapping class group, we will generalize to C^0 settings a result of Seidel concerning the non-triviality of the mapping class of this symplectomorphism. We will indeed prove that the generalized Dehn twist is infinite order in the group of the connected component of symplectic homeomorphisms. Doing so, we prove the non-triviality of the C^0 symplectic mapping class group of some Liouville domains. | ||
| Jan 19 | Razvan Gurau | How should we encode the metric of a tringulation? |
| Slides | ||
| Feb 2 | Beatrice Pozzetti | Structures on surfaces |
| I will discuss several structures on topological surfaces, and their relation with character varieties and their compactifications. | ||
| Feb 16 | Christoph Schnörr | A Brief Review of some CP6 Topics |
| This talk gives a brief overview of current research directions in machine learning in connection with deep networks, including a brief historical account of research paradigms of AI in computer vision. The aim is to stimulate discussion among the members of the lunch seminar about the relation of mathematics, machine learning and data analysis, from the viewpoint of STRUCTURES. | ||
Summer semester 2021
| Date | Name | Title of talk |
|---|---|---|
| April 21 | Anna Wienhard, Johannes Walcher | What is CP7? |
| May 5 | Johanna Bimmermann | Magnetic Systems in Symplectic Geometry |
| As well known in physics the phase space of a classical system carries a canonic symplectic structure which together with a Hamiltonian function determines the dynamics of the system. In this lunch break we will investigate the question what happens if we perturb the canonic symplectic structure by a so called magnetic term. Slides | ||
| May 19 | Giulio Belletti | Quantum probabilities on the space of metrics on S^2 |
| I will discuss a work in progress with F. Costantino and E. Levine concerning the problem of defining a probability on the space of metrics on the sphere. This will rely on the Turaev-Viro invariant, an invariant of graphs in 3-manifolds that comes from a Topological Quantum Field Theory. | ||
| June 2 | Simone Noja | Local and Global Problems in Supergeometry |
| Triggered by the advent of supersymmetry, supergeometry studies varieties characterized by a set of commuting - or bosonic - and anticommuting - or femionic - local coordinates. In this seminar I will give an overview of some of its most peculiar aspects and their significance to the physics of strings and supersymmetric field theories. | ||
| June 16 | Xian Dai | The Weil Petersson Metric Geometry and Its Generalization |
| In this talk, I will give an overview of the classical Weil Petersson metric which is a Riemannian metric defined on Teichmüller space. Many of the important and beautiful properties of Weil Petersson geometry from different aspects will be described. In the end, I will talk about a natural generalization of the Weil Petersson metric in the Higher Teichmüller space and ask some potential problems about it. | ||
| June 23 | Arthur Hebecker | The Measure Problem of Eternal Inflation and Ideas for a Quantum Mechanical Approach |
| I will start with a very brief tour of String-Theory-Landscape, Multiverse and de Sitter space, just enough to explain how Eternal Inflation can arise and why it leads to a problem of predictivity or Measure Problem. Then some preliminary ideas concerning a quantum mechanical approach to overcoming this problem will be explained. | ||
| July 7 | Carmen Rovi | Relating Cut and Paste invariants and TQFTs |
| Two smooth, oriented, closed manifolds M and N are cut and paste equivalent if one can obtain N by a series of cut and paste operations from M. Cut and paste controlled invariants (SKK invariants) are functions on the set of smooth manifolds whose values on cut and paste equivalent manifolds differ by an error term depending only on the gluing diffeomorphisms. In this talk, I will present the construction of a group homomorphism between the group of invertible TQFTs and the group of SKK invariants and describe how these groups fit into an exact sequence. | ||
| July 21 | Discussion on continuation in fall | |
Mailing list
We have a mailing list for the seminar. If you want to be added to the list, send an email to STRUCTURES-CP7-subscribe-request@listserv.uni-heidelberg.de (content and title does not matter).
Contact
Organizers: Luca Battistella, Alexandre Jannaud and Anja Randecker
