11.1 Primäre und hyperprimäre Zahlen
Um die diesbezüglichen Fragen Artins zu verstehen, ist es notwendig, die bei
Hasse und Artin verwendeten Bezeichnungen und die Terminologie zu kennen. k
sei ein Zahlkörper, der die m-ten Einheitswurzeln enthält.  bezeichnet eine in m
aufgehende Primzahl, und
bezeichnet eine in m
aufgehende Primzahl, und  n die genaue Potenz, mit der
n die genaue Potenz, mit der  in m aufgeht.
in m aufgeht.  ist
eine primitive
ist
eine primitive  -te Einheitswurzel und
-te Einheitswurzel und  = 1 -
= 1 -  der Primteiler von
der Primteiler von  im Körper der
im Körper der  -ten Einheitswurzeln. Artin fragt, welchen Exponenten
t man benötigt, um aus einer Kongruenz
-ten Einheitswurzeln. Artin fragt, welchen Exponenten
t man benötigt, um aus einer Kongruenz 
 1 mod
1 mod  t schliessen zu
können, dass
t schliessen zu
können, dass  primär für
primär für  ist, d.h. dass
ist, d.h. dass  teilerfremd ist zum Führer von
k(
teilerfremd ist zum Führer von
k(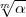 ).
Und entsprechend, wenn „primär“ durch „hyperprimär“ ersetzt wird; das
bedeutet, dass jeder Primteiler von
).
Und entsprechend, wenn „primär“ durch „hyperprimär“ ersetzt wird; das
bedeutet, dass jeder Primteiler von  im Kummerschen Körper k(
im Kummerschen Körper k(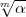 )
vollzerlegt ist. (Artin bezeichnet die Primteiler von
)
vollzerlegt ist. (Artin bezeichnet die Primteiler von  im Körper k mit dem
Buchstaben
im Körper k mit dem
Buchstaben  i.) Fragen dieser Art sind für explizite Reziprozitätsformeln von
Bedeutung.
i.) Fragen dieser Art sind für explizite Reziprozitätsformeln von
Bedeutung.
Möglicherweise hat Artin nur den Fall m =  n und k =
n und k =  (
(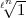 ) im Auge. In
jedem Falle ist aber seine Behauptung nicht richtig, dass man mit (1 -
) im Auge. In
jedem Falle ist aber seine Behauptung nicht richtig, dass man mit (1 -  )
) als
Modul auskommt (also t =
als
Modul auskommt (also t =  ). Das hat Artin offenbar ziemlich bald selbst
bemerkt, wie aus seinem nächsten Brief Nr. 12 vom 29.7.1927 hervorgeht. Dort
vermutet er, dass (1 -
). Das hat Artin offenbar ziemlich bald selbst
bemerkt, wie aus seinem nächsten Brief Nr. 12 vom 29.7.1927 hervorgeht. Dort
vermutet er, dass (1 - )
) n
ausreicht. Im allgemeinen scheint wohl auch dies nicht
richtig zu sein. Die genauen Exponenten wurden später von Hasse in Teil II
seines Klassenkörperberichts [Has30a] angegeben; vgl. §9, Sätze X und XI jenes
Berichts.
n
ausreicht. Im allgemeinen scheint wohl auch dies nicht
richtig zu sein. Die genauen Exponenten wurden später von Hasse in Teil II
seines Klassenkörperberichts [Has30a] angegeben; vgl. §9, Sätze X und XI jenes
Berichts.
Vgl. auch den Brief Nr.14 vom 6.8.1927 und 14.2.
 bezeichnet eine in m
aufgehende Primzahl, und
bezeichnet eine in m
aufgehende Primzahl, und  n die genaue Potenz, mit der
n die genaue Potenz, mit der  in m aufgeht.
in m aufgeht.  ist
eine primitive
ist
eine primitive  -te Einheitswurzel und
-te Einheitswurzel und  = 1 -
= 1 -  der Primteiler von
der Primteiler von  im Körper der
im Körper der  -ten Einheitswurzeln. Artin fragt, welchen Exponenten
t man benötigt, um aus einer Kongruenz
-ten Einheitswurzeln. Artin fragt, welchen Exponenten
t man benötigt, um aus einer Kongruenz 
 1 mod
1 mod  t schliessen zu
können, dass
t schliessen zu
können, dass  primär für
primär für  ist, d.h. dass
ist, d.h. dass  teilerfremd ist zum Führer von
k(
teilerfremd ist zum Führer von
k(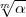 ).73
Und entsprechend, wenn „primär“ durch „hyperprimär“ ersetzt wird; das
bedeutet, dass jeder Primteiler von
).73
Und entsprechend, wenn „primär“ durch „hyperprimär“ ersetzt wird; das
bedeutet, dass jeder Primteiler von  im Kummerschen Körper k(
im Kummerschen Körper k(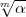 )
vollzerlegt ist. (Artin bezeichnet die Primteiler von
)
vollzerlegt ist. (Artin bezeichnet die Primteiler von  im Körper k mit dem
Buchstaben
im Körper k mit dem
Buchstaben  i.) Fragen dieser Art sind für explizite Reziprozitätsformeln von
Bedeutung.
i.) Fragen dieser Art sind für explizite Reziprozitätsformeln von
Bedeutung.