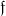 (
( ,K/k) im Abelschen Falle bekannt? Wenn nicht, so ist sie
immerhin noch eine kleine Ergänzung auch zur Klassenkörpertheorie.
29
,K/k) im Abelschen Falle bekannt? Wenn nicht, so ist sie
immerhin noch eine kleine Ergänzung auch zur Klassenkörpertheorie.
29
Lieber Herr Hasse!
Vielen Dank für Ihren freundlichen Brief. Was die Veröffentlichung in Crelle betrifft, so möchte ich Ihnen folgendes vorschlagen:27
Ich hatte schon vor, die Untersuchungen in zwei Teile zu zerlegen: 1.)Gruppentheoretische Struktur der Diskriminante algebraischer Zahlkörper. 2.) Zur Theorie der L-Reihen mit allgemeinen Gruppencharakteren. Diese Teilung will ich vornehmen, weil mir 1.) von allgemeiner Wichtigkeit zu sein scheint, unabhängig von der Anwendung bei 2.). Ich verspreche mir von einem weiteren Ausbau der Führertheorie noch sehr viele weitere Resultate. Z.B. habe ich eine kleine Hoffnung für den Klassenkörperturm. In einer Untersuchung über die L-Reihen aber würde das völlig untergehen. Publiziere ich es aber selbständig, so werden es doch vielleicht einige Leute beachten, die beim Lesen des Titels L-Reihe die Arbeit mit Grauen beiseite legen würden.
Ich möchte Ihnen nun vorschlagen, dass ich 1.) bei Ihnen drucken lasse, 2.) aber aus alter Anhänglichkeit in Hamburg. Das passt auch insofern ganz gut, als ja bei Ihnen Ihre eigene Führerarbeit28 erschienen ist, in Hamburg aber andrerseits die erste Publikation über L-Reihen. Erscheint Ihnen die Trennung und diese Gesichtspunkte nicht auch richtig? Die genaue Niederschrift werde ich erst am 15.Oktober machen können, da ich nicht wesentlich früher in Hamburg eintreffen werde und vorher doch nicht zu einer Ausarbeitung komme.
Bei dieser Gelegenheit möchte ich noch fragen: War Ihnen die
Formel für 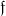 (
( ,K/k) im Abelschen Falle bekannt? Wenn nicht, so ist sie
immerhin noch eine kleine Ergänzung auch zur Klassenkörpertheorie.
29
,K/k) im Abelschen Falle bekannt? Wenn nicht, so ist sie
immerhin noch eine kleine Ergänzung auch zur Klassenkörpertheorie.
29
Nun komme ich meinerseits mit einer grossen Bitte. Wie Sie vielleicht erfahren haben, habe ich die weitere Herausgabe der Sammlung Hilb bei der Akademischen Verlagsgesellschaft übernommen. Nun hätte ich da gar zu gerne auch ein Buch von Ihnen. Wäre es Ihnen nicht möglich in dieser Sammlung ein Buch über komplexe Multiplikation zu schreiben? Ich habe schon mit dem Verleger verhandelt. Wir nehmen jeden Beitrag von Ihnen. Ich denke hauptsächlich an komplexe Multiplikation, weil da bisher überhaupt kein brauchbares Buch vorliegt. Aber auch alles sonstige würde ich gerne nehmen. Wie denken Sie darüber. Erfüllen Sie doch meine Bitte! Einen Termin würde ich Ihnen auch nicht stellen wollen, da ich weiss wie sehr Sie bisher schon mit dem „Bericht“ überlastet worden sind. Das würde ich alles Ihnen überlassen.30
Nun komme ich zu  2-primär .31
Ich gehe von Ihrer Formel
2-primär .31
Ich gehe von Ihrer Formel
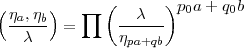
 n aus, und schreibe sie mir zunächst auf unsere alte
n aus, und schreibe sie mir zunächst auf unsere alte  a-Basis um. Da
wird sie einfacher. Beim Umschreiben braucht man nicht den Wert von
a-Basis um. Da
wird sie einfacher. Beim Umschreiben braucht man nicht den Wert von 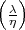 einzusetzen, sondern kann alles direkt machen. Man erhält
einzusetzen, sondern kann alles direkt machen. Man erhält
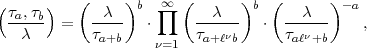
 = 2 leichte Modifikation. Lassen wir aber
= 2 leichte Modifikation. Lassen wir aber  ungerade.
ungerade.
Sind a und b prim zu  , so folgt aus unserer Arbeit Punkt 8, dass
, so folgt aus unserer Arbeit Punkt 8, dass
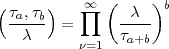
 n aber folgt für zu
n aber folgt für zu  primes b:
primes b:
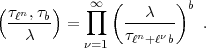
Im ersten Fall ist a + b < 2 n, also nach Punkt 15 unserer Arbeit:
n, also nach Punkt 15 unserer Arbeit:
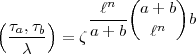
 teilbares a + b des Intervalls
teilbares a + b des Intervalls
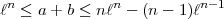
Im Falle n = 2 bedeutet das:  2 < a + b <
2 < a + b <  2 + (
2 + ( - 1)
- 1) , also:
, also:
1.) a + b =  2, wo dann
2, wo dann 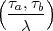 =
=  b ist,
b ist,
2.) a + b =  2 + k
2 + k mit 1 < k <
mit 1 < k <  - 1, wo dann:
- 1, wo dann:
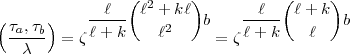
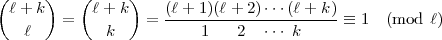
 + k
+ k  k (mod
k (mod  ), so dass
), so dass
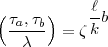
 2 verstanden.) Bleibt noch
2 verstanden.) Bleibt noch 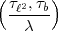 zu
bestimmen. Im Produkt genügt dann
zu
bestimmen. Im Produkt genügt dann  = 1, so dass:
= 1, so dass:
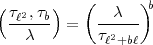
 - 1 und es ist:
- 1 und es ist:
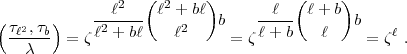
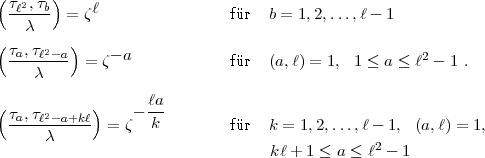
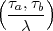 = 1 für die anderen
= 1 für die anderen  a,
a, b unserer Basis.
b unserer Basis.
Ein primäres  kann gleich in der Form
kann gleich in der Form  =
= 
 2
2 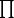 (a,
(a, )=1
1<a<
)=1
1<a< 2-1
2-1  axa angesetzt
werden, wo die xa zu bestimmen sind.
axa angesetzt
werden, wo die xa zu bestimmen sind.
Da 
 1 (mod
1 (mod  1
1 =
= 
 2
) sein muss, sind dabei die xa alle durch
2
) sein muss, sind dabei die xa alle durch  teilbar. Nun
muss gelten:
teilbar. Nun
muss gelten:
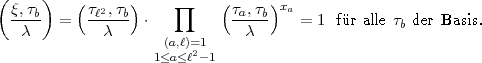
 2 ist nach der Tabelle vermöge xa
2 ist nach der Tabelle vermöge xa  0 (mod
0 (mod  ) schon alles erfüllt. Sei also b
prim zu
) schon alles erfüllt. Sei also b
prim zu  . Da die xa durch
. Da die xa durch  teilbar sind, folgt aus der Tabelle, dass vom
Produkt nur das eine Glied mit a =
teilbar sind, folgt aus der Tabelle, dass vom
Produkt nur das eine Glied mit a =  2 - b stehen bleibt. Man hat nun zu
unterscheiden:
2 - b stehen bleibt. Man hat nun zu
unterscheiden:
1.) b = 1,2,… - 1; dann lautet die Gleichung:
- 1; dann lautet die Gleichung:
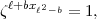
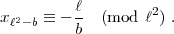
 + 1; dann lautet sie:
+ 1; dann lautet sie:
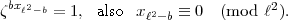
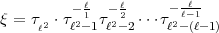
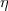 2
2 2 schon primär ist, kann
2 schon primär ist, kann 
 2 ersetzt werden durch
2 ersetzt werden durch 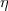
 2. Potenziert man aus
und lässt analog alles weg was jenseits des Primäritätsmoduls liegt, so erhält
man:
2. Potenziert man aus
und lässt analog alles weg was jenseits des Primäritätsmoduls liegt, so erhält
man:
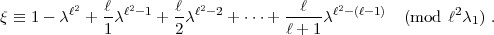
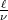 nach dem Modul
nach dem Modul  2 behandelt werden. Nun ist
(
2 behandelt werden. Nun ist
(

 )
=
)
=  .
.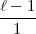 .
.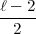

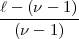
 (-1)
(-1) -1
-1 (mod
(mod  2) für 1 <
2) für 1 <  <
<  - 1.
Also ist:
- 1.
Also ist: 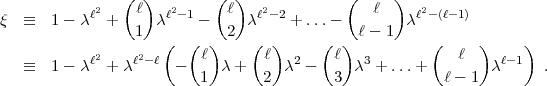
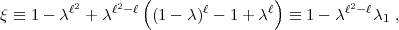
 1 = 1 -
1 = 1 -  1 = 1 - (1 -
1 = 1 - (1 -  )
) gesetzt ist. Also ist die
Zahl:32
gesetzt ist. Also ist die
Zahl:32
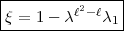
 2-primär im
2-primär im  2-ten Kreiskörper und somit
2-ten Kreiskörper und somit  2-primär in jedem Oberkörper, also
auch
2-primär in jedem Oberkörper, also
auch  2-primär für jeden Primteiler
2-primär für jeden Primteiler  von
von  in jedem Oberkörper des Kreiskörpers.
Da sie /
in jedem Oberkörper des Kreiskörpers.
Da sie / 1 (mod
1 (mod 
 1
1 ) ist, ist sie die gesuchte Basis für die primären
Zahlen.
) ist, ist sie die gesuchte Basis für die primären
Zahlen.
Da haben Sie also den Beweis. Wie Sie sehen, bin ich mit dem Kopf durch die
Wand gegangen. Das habe ich auch noch im Falle  3-primär getan. Ergebnis: Ein
ellenlanger Ausdruck für
3-primär getan. Ergebnis: Ein
ellenlanger Ausdruck für  , dem man weiter nichts ansehen kann. Es lohnt sich
also nicht ihn hinzuschreiben. Vielleicht lag das an meiner Ungeschicklichkeit, und
vielleicht erraten Sie nun das Richtige. Ich glaube hier kommt es aufs Erraten an.
In der Führersache und der Funktionalgleichung musste ich auch alles
erraten.
, dem man weiter nichts ansehen kann. Es lohnt sich
also nicht ihn hinzuschreiben. Vielleicht lag das an meiner Ungeschicklichkeit, und
vielleicht erraten Sie nun das Richtige. Ich glaube hier kommt es aufs Erraten an.
In der Führersache und der Funktionalgleichung musste ich auch alles
erraten.
Welche Behauptungen stellt eigentlich Weddle33 auf? Ich schrieb Ihnen schon, dass mir seine Arbeit unzugänglich ist.
Darf ich Sie endlich noch bitten, mir ganz kurz die Ergebnisse von Frl. Taussky zu erzählen? Das interessiert mich sehr.34
Ja, Sie werden enttäuscht sein von dem  2-primär, aber vielleicht finden Sie in
dem Brief doch noch etwas brauchbares.
2-primär, aber vielleicht finden Sie in
dem Brief doch noch etwas brauchbares.
Darf ich Sie nun noch bitten, mir nach Reichenberg zu schreiben: Adresse: Artin, bei Dr. Hübner, Reichenberg Č.S.R., Felgenhauerstrasse 20.
Ich verreise nämlich in den nächsten Tagen dorthin.
Mit den besten Grüssen auch an Frau Gemahlin und auch von meiner Frau
Ihr Artin
Kommentare zum Brief Nr.31: