32 10.10.1930, Brief von Artin an Hasse
Hamburg-Fuhlsbüttel
Kleekamp 3
I
Lieber Herr Hasse!
Vielen Dank für Ihre ausserordentlich interessanten
Mitteilungen.
Sie sind da wirklich einen grossen Schritt vorwärts gekommen. Ich bin jetzt
leider mit der Ausarbeitung (allerdings nur im Kopf) der schwebenden
Dinge
so in Anspruch genommen, dass ich das noch nicht vollständig verdauen konnte.
Ausserdem komme ich hier nicht recht zum Arbeiten. In Hamburg will ich mich
dann ausführlicher damit beschäftigen.
Sie fragen nach den Kongruenzen für die
vi.
Ich glaube nicht, dass diese Kongruenzen auch im allgemeinen galois’schen Fall
stimmen, sondern dass sie aus anderen Sätzen folgen. Wenn Sie den Nenner im
Exponenten von 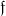 (
( ) betrachten, so handelt es sich bei der Ganzheit um eine
Teilbarkeit durch e = e0pR1. Die Teilbarkeit durch e0 konnte ich durch einen
einfachen Hilfssatz erledigen, der im abelschen Fall die Teilbarkeit der vi durch e0
nach sich zieht (dieser Hilfssatz hat mir allerdings zuerst die grössten Schwierigkeiten
verursacht).
) betrachten, so handelt es sich bei der Ganzheit um eine
Teilbarkeit durch e = e0pR1. Die Teilbarkeit durch e0 konnte ich durch einen
einfachen Hilfssatz erledigen, der im abelschen Fall die Teilbarkeit der vi durch e0
nach sich zieht (dieser Hilfssatz hat mir allerdings zuerst die grössten Schwierigkeiten
verursacht).
Der unangenehme Teil ist die Teilbarkeit durch pR1. Im abelschen Fall besagt
diese genau Ihre Kongruenzen. Ich habe lange versucht diese Teilbarkeit direkt zu
zeigen, bin aber viel zu ungeschickt um es auch nur im abelschen Fall zu können.
Nun haben Sie das aber getan. Ich glaube, an der Hand Ihres Beweises würde mir
vielleicht der direkte Nachweis gelingen. Nun habe ich aber kein Separatum Ihrer
Führerarbeit. Auch in Hamburg habe ich keines. Darf ich Sie also herzlich
bitten mir eines nach Hamburg zu senden, damit ich versuchen kann
diese Teilbarkeitsfrage direkt zu entscheiden? Ich sehe schon, dass es mir
ohne die neue Idee, die in Ihrer Arbeit stecken muss nicht glücken wird.
Ausserdem werde ich die Arbeit wahrscheinlich auch wegen des Zitats
benötigen.
Ich will Ihnen kurz zeigen, auf welchem Umweg ich die Teilbarkeit durch pR1
doch noch erzwungen habe. Es sei K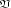 der erste Verzweigungskörper. Man sieht
sofort, dass der Exponent von
der erste Verzweigungskörper. Man sieht
sofort, dass der Exponent von  in
in 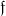 (
( ,K/k) im „Wesentlichen“ derselbe ist, wie
der von
,K/k) im „Wesentlichen“ derselbe ist, wie
der von 
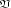 in
in 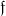 (
( ,K/K
,K/K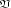 ), wenn
), wenn 
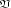 der Primteiler von
der Primteiler von  in K
in K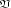 ist. Also genügt
es, im Körper K/K
ist. Also genügt
es, im Körper K/K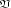 die Ganzheit des Exponenten zu zeigen. Damit ist man auf
den Fall einer Gruppe von Primzahlpotenzordnung zurückgekommen. Da
nun jede Darstellung einer solchen Gruppe eine monomiale ist, reduziert
sich endlich der Nachweis auf den Abelschen Fall und damit bin ich am
Ende.
die Ganzheit des Exponenten zu zeigen. Damit ist man auf
den Fall einer Gruppe von Primzahlpotenzordnung zurückgekommen. Da
nun jede Darstellung einer solchen Gruppe eine monomiale ist, reduziert
sich endlich der Nachweis auf den Abelschen Fall und damit bin ich am
Ende.
Ich habe natürlich versucht diesen Umweg zu vermeiden. Wie ich schon sagte,
gelang mir aber der Nachweis nicht einmal im Abelschen Fall. Daher möchte ich
gerne den Beweis Ihrer Kongruenzen kennen lernen.
Welche Voraussetzungen aus der Klassenkörpertheorie muss ich nun machen?
Für den formalen Teil keine. Für die Ganzheit des Exponenten entweder Ihre
Kongruenzen, oder die Diskriminanten-Führerformel , aus der man sie rückwärts
gewinnen kann. Für die Tatsache aber, dass im abelschen Fall 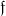 (
( ) wirklich der Führer
ist, die Diskriminanten-Führerformel also nach Belieben Ihren Beweis oder den
Heckeschen.
Es kann aber sein, dass sich jetzt auch einige Vereinfachungen der
Diskriminanten-Führerformel ergeben. Das kann ich aber erst nach Kenntnis Ihres
Beweises sagen.
) wirklich der Führer
ist, die Diskriminanten-Führerformel also nach Belieben Ihren Beweis oder den
Heckeschen.
Es kann aber sein, dass sich jetzt auch einige Vereinfachungen der
Diskriminanten-Führerformel ergeben. Das kann ich aber erst nach Kenntnis Ihres
Beweises sagen.
Ich schreibe das alles nicht so sehr ausführlich, da Sie ja doch bald mein
Manuskript in Händen haben werden.
Ich will lieber noch einiges erzählen was hinzugekommen ist.
1.) Bei gegebenem Wert von  (1) (dem Grad der Darstellung), gegebenem
Grundkörper k und gegebenem Ideal
(1) (dem Grad der Darstellung), gegebenem
Grundkörper k und gegebenem Ideal  aus k, hat die Gleichung
aus k, hat die Gleichung 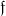 (
( ) =
) =  nur
„endlich viele“ Lösungen. D.h. es gibt nur endlich viele Oberkörper K, in denen
nur
„endlich viele“ Lösungen. D.h. es gibt nur endlich viele Oberkörper K, in denen
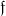 (
( ) vorkommen kann (dabei K immer kleinstmöglich). Der Beweis ist noch sehr
umständlich.
) vorkommen kann (dabei K immer kleinstmöglich). Der Beweis ist noch sehr
umständlich.
2.) Zur Theorie der L-Reihen. Bildet man L-Reihen mit rationalen
Charakteren, d.h. Charakteren  (
( ) deren Werte rational sind und die nicht
einfach zu sein brauchen, so hat man in ihnen die „Bestandteile“ der
Zetafunktionen. Sie lassen sich umgekehrt durch Zetafunktionen ausdrücken so
dass zu ihrer Fortsetzbarkeit nicht das Rez[iprozitäts]ges[etz] herangezogen
werden muss. Alles geht hier ohne Klassenkörpertheorie. Da nun die
Anzahl der rationalen Charaktere gleich der Anzahl der Abteilungen in
der Gruppe ist, hat man hier genau die für die Frobeniusdichtigkeiten
erforderlichen Funktionen. Was die
) deren Werte rational sind und die nicht
einfach zu sein brauchen, so hat man in ihnen die „Bestandteile“ der
Zetafunktionen. Sie lassen sich umgekehrt durch Zetafunktionen ausdrücken so
dass zu ihrer Fortsetzbarkeit nicht das Rez[iprozitäts]ges[etz] herangezogen
werden muss. Alles geht hier ohne Klassenkörpertheorie. Da nun die
Anzahl der rationalen Charaktere gleich der Anzahl der Abteilungen in
der Gruppe ist, hat man hier genau die für die Frobeniusdichtigkeiten
erforderlichen Funktionen. Was die  -Relationen betrifft, so erhält man das
ziemlich abschliessende Ergebnis: Die Anzahl der unabhängigen unter den
-Relationen betrifft, so erhält man das
ziemlich abschliessende Ergebnis: Die Anzahl der unabhängigen unter den
 -Funktionen der Unterkörper ist gleich der Anzahl der Abteilungen der
Gruppe.
-Funktionen der Unterkörper ist gleich der Anzahl der Abteilungen der
Gruppe.
3.) Ich erwähnte eben: Die Anzahl der rationalen Charaktere ist gleich der Anzahl
der Abteilungen. Dieser Satz war mir nicht bekannt und ich glaube auch dass er neu
ist.
Analog kann man z.B. genau den Charakterenkörper irgend einer Gruppe
angeben:
Sei n die Ordnung der Gruppe. Man suche alle Restklassen i (mod n) mit der
Eigenschaft, dass für alle  aus
aus 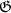 gilt
gilt  ~
~  i (wo ~ bedeutet zur gleichen Klasse
konjugierter Elemente). Diese Restklassen i bilden eine Untergruppe g der Gruppe G
aller Restklassen (mod n) , also der Gruppe des n-ten Kreiskörpers. Zu g gehört
nun ein gewisser Unterkörper k des Kreiskörpers und dieser ist genau der
Charakterenkörper.
i (wo ~ bedeutet zur gleichen Klasse
konjugierter Elemente). Diese Restklassen i bilden eine Untergruppe g der Gruppe G
aller Restklassen (mod n) , also der Gruppe des n-ten Kreiskörpers. Zu g gehört
nun ein gewisser Unterkörper k des Kreiskörpers und dieser ist genau der
Charakterenkörper.
Kennen Sie diese und ähnliche Sätze? Ich glaube sie sind neu.
Die Umrechnung Ihrer Formel auf die  a-Basis ist in der Tat rein formal. Ich
halte die Angelegenheit nicht für so wichtig um sie zu schreiben. Ich kann sie
Ihnen ja später einmal mitteilen.
a-Basis ist in der Tat rein formal. Ich
halte die Angelegenheit nicht für so wichtig um sie zu schreiben. Ich kann sie
Ihnen ja später einmal mitteilen.
Wir fahren in den nächsten Tagen weg und kommen am 14.Oktober endgültig
nach Hamburg.
Darf ich meine Bitte um ein Separatum nochmals erneuern und Sie darum
ersuchen es nach Hamburg zu schicken?
Mit vielen Grüssen auch von meiner Frau und besten Empfehlungen an Ihre
Frau Gemahlin.
Herzlichst Ihr
Artin
P.S. Ich vergass soeben das Wichtigste, nämlich Ihnen für Ihre
halbe Zusage zur komplexen Multiplikation zu danken. Mir würde
wirklich sehr viel daran liegen, das Buch in die Sammlung zu bekommen
und wir können ja vorläufig die Sache noch vertagen und ihre weitere
Entwicklung abwarten. Jedenfalls will ich Sie nicht mit einem Kontrakt
plagen. Darf ich Sie nach den Bedingungen bei Springer fragen und auch
danach, in welchen Punkten Sie gerne Günstigeres wünschen würden?
Seien Sie überzeugt, dass ich alles daransetzen werde um Ihre Wünsche zu
befriedigen.
Kommentare zum Brief Nr.32:
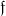 (
( ) betrachten, so handelt es sich bei der Ganzheit um eine
Teilbarkeit durch e = e0pR1. Die Teilbarkeit durch e0 konnte ich durch einen
einfachen Hilfssatz erledigen, der im abelschen Fall die Teilbarkeit der vi durch e0
nach sich zieht (dieser Hilfssatz hat mir allerdings zuerst die grössten Schwierigkeiten
verursacht).46
) betrachten, so handelt es sich bei der Ganzheit um eine
Teilbarkeit durch e = e0pR1. Die Teilbarkeit durch e0 konnte ich durch einen
einfachen Hilfssatz erledigen, der im abelschen Fall die Teilbarkeit der vi durch e0
nach sich zieht (dieser Hilfssatz hat mir allerdings zuerst die grössten Schwierigkeiten
verursacht).46