41.1 Fortsetzung der L-Reihen
Der Brief ist offenbar die Antwort auf eine Anfrage Hasses nach einem
einfachen Beweis der Fortsetzbarkeit der Weberschen L-Reihen. Wie es scheint,
bereitet Hasse seine Vorlesung über Klassenkörpertheorie vor, die er im
Sommersemester 1932 dann gehalten hat. Es geht um die Fortsetzbarkeit
der L-Reihen L(s, ) auf die gesamte rechte Halbebene. Dabei ist eine
Kongruenzgruppe H in k gegeben, und
) auf die gesamte rechte Halbebene. Dabei ist eine
Kongruenzgruppe H in k gegeben, und  ist ein Charakter der zugehörigen
Faktorgruppe nach H. Die Situation ist also wie im Brief Nr. 38 vom 16.6.1931,
vgl. 38.3.1. Nur ist jetzt kein Oberkörper K von k vorgegeben.
ist ein Charakter der zugehörigen
Faktorgruppe nach H. Die Situation ist also wie im Brief Nr. 38 vom 16.6.1931,
vgl. 38.3.1. Nur ist jetzt kein Oberkörper K von k vorgegeben.
In der Ausarbeitung seiner Vorlesung [Has33c] diskutiert Hasse die Frage, ob
L(1, )≠0 ist für
)≠0 ist für  ≠1. Er stellt fest, dass es höchstens einen Charakter
≠1. Er stellt fest, dass es höchstens einen Charakter  ≠1 geben
kann, für welchen L(1,
≠1 geben
kann, für welchen L(1, ) = 0 ist, und dieser müsste reell sein. Dies aber tritt
nicht ein, sagt Hasse:
) = 0 ist, und dieser müsste reell sein. Dies aber tritt
nicht ein, sagt Hasse:
„Es gibt zwei wesentlich verschiedene Methoden zum Beweis.
Der eine, kürzere, ist funktionentheoretisch und beruht auf einem
Satz über Dirichletsche Reihen mit positiven Koeffizienten. Man
braucht aber überdies die Fortsetzbarkeit aller L-Funktionen in
die rechte Halbebene, die nur mit großem Aufwand zu gewinnen
ist. Die andere Methode ist arithmetisch-körpertheoretisch und
führt in die Klassenkörpertheorie. Diese letztere werden wir
anwenden.“
Wie es scheint, möchte Hasse wissen, ob man auch ohne Klassenkörpertheorie,
aber auch ohne großen sonstigen Aufwand, einen Beweis für das Nichtverschwinden
der L-Funktionen für s = 1 und  ≠1 finden kann. Dann würde ja daraus nach der
Dirichletschen Methode direkt abzulesen sein, dass die Primideale in H und auch
die in jeder Nebenklasse nach H die Dichte
≠1 finden kann. Dann würde ja daraus nach der
Dirichletschen Methode direkt abzulesen sein, dass die Primideale in H und auch
die in jeder Nebenklasse nach H die Dichte 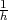 besitzen. Das konnte ja Artin nach
seiner im Brief Nr.38 angegebenen Methode nur dann, wenn er den dort mit K
bezeichneten Erweiterungskörper hat.
besitzen. Das konnte ja Artin nach
seiner im Brief Nr.38 angegebenen Methode nur dann, wenn er den dort mit K
bezeichneten Erweiterungskörper hat.
Artin hat, wie wir sehen, auch keinen Erfolg bei seinen Versuchen
gehabt. Wenn er schreibt, dass man nur die Fortsetzbarkeit für Realteil
R(s) >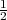 benötige, dann bezieht er sich auf die übliche Schlussweise,
dass man ja nur quadratische, also reelle Charaktere
benötige, dann bezieht er sich auf die übliche Schlussweise,
dass man ja nur quadratische, also reelle Charaktere  in Betracht zu
ziehen braucht. Für diese wäre es ausreichend, wenn man s =
in Betracht zu
ziehen braucht. Für diese wäre es ausreichend, wenn man s = 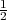 setzen
könnte.
setzen
könnte.
 ) auf die gesamte rechte Halbebene. Dabei ist eine
Kongruenzgruppe H in k gegeben, und
) auf die gesamte rechte Halbebene. Dabei ist eine
Kongruenzgruppe H in k gegeben, und  ist ein Charakter der zugehörigen
Faktorgruppe nach H. Die Situation ist also wie im Brief Nr. 38 vom 16.6.1931,
vgl. 38.3.1. Nur ist jetzt kein Oberkörper K von k vorgegeben.
ist ein Charakter der zugehörigen
Faktorgruppe nach H. Die Situation ist also wie im Brief Nr. 38 vom 16.6.1931,
vgl. 38.3.1. Nur ist jetzt kein Oberkörper K von k vorgegeben.
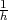 besitzen. Das konnte ja Artin nach
seiner im Brief Nr.
besitzen. Das konnte ja Artin nach
seiner im Brief Nr.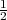 benötige, dann bezieht er sich auf die übliche Schlussweise,
dass man ja nur quadratische, also reelle Charaktere
benötige, dann bezieht er sich auf die übliche Schlussweise,
dass man ja nur quadratische, also reelle Charaktere 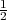 setzen
könnte.
setzen
könnte.