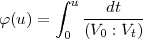
In diesem Abschnitt wollen wir einen Überblick geben über die Aktivitäten, die Artins Idee, seine Führertheorie unabhängig von der Klassenkörpertheorie zu begründen, umzusetzen versuchten. Die Noethersche Arbeit [Noe32], die allerdings nur den zahm verzweigten Fall behandeln konnte, haben wir schon erwähnt. Vgl. 30.1.3 und 33.3.
Im Jahr 1934 erschien Hasses Arbeit [Has34b] mit dem Titel: „Normenresttheorie galoisscher Zahlkörper mit Anwendungen auf Führer und Diskriminante abelscher Zahlkörper.“ In gewisser Weise kann dies als eine Neufassung der bereits erwähnten Führer-Arbeit [Has30d] angesehen werden (vgl. Kommentare 31.2 und 32.1). Jetzt aber wird die Untersuchung systematisch auf galoissche Körper ausgedehnt, die nicht notwendig abelsch sind. Es ist unschwer zu erkennen, dass diese Arbeit unmittelbar beeinflusst wurde durch die Frage Artins, wie denn die Hasseschen Kongruenzen (47) (Seite 557) im galoisschen Fall aussehen würden. Denn im vorliegenden Brief sagt Artin: „Wie aber der entsprechende Satz allgemein lautet, davon habe ich keine Ahnung“. Hasse versucht es nun in [Has34b] mit einer genauen Untersuchung der Normenreste im galoisschen Fall.
Die wesentlichen Hilfsmittel dazu sind, erstens, seine eigenen Arbeiten zum lokalen Aufbau der Normenresttheorie, und zweitens, die Ergänzung von Herbrand zur Hilbertschen Verzweigungstheorie für galoissche Körper [Her31a]. In dieser Arbeit führt Herbrand die sogenannte „obere Numerierung“ der Verzweigungsgruppen ein. Nach [Has34b] kann dies durch eine stückweise lineare und monotone Funktion, die sogenannte „Hasse-Funktion“, beschrieben werden, die man heute meist in der Form
|
|
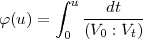schreibt. Dabei wird für reelles t die Verzweigungsgruppe V t = V i gesetzt, wenn i
die kleinste ganze Zahl > t ist. Sei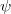 
die Umkehrfunktion von 
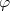. Die
Herbrandsche Numerierung der Verzweigungsgruppen wird dann gegeben
durch
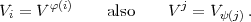
Nach Herbrand passt sich diese Numerierung dem Übergang zu galoisschen Teilkörpern an, also zu Faktorgruppen der Galoisgruppe. Hasse untersucht nun in [Has34b] systematisch den Zusammenhang dieser Herbrandschen Numerierung mit den Normenresten. Es ist offensichtlich (obwohl Hasse das nicht explizit sagt), dass er dabei zum Ziel hat, eine Verallgemeinerung der Kongruenzen (47), die er vom abelschen Fall her ja kannte, für beliebige galoissche Körper zu finden, um damit vielleicht das Problem der Artinschen Führer lösen zu können. Zwar gelingt ihm das nicht, aber dennoch ist diese Arbeit zu den bedeutenden Fortschritten in der von Hensel begonnenen lokalen Theorie der Normenreste zu zählen. Eine systematische Darstellung im Rahmen der Theorie der lokalen Körper findet man in Serres „Corps locaux“ [Ser62].
Im abelschen Falle findet Hasse in [Has34b] seine Kongruenzen (47) wieder, allerdings wiederum nur mit Hilfe der Klassenkörpertheorie. Diesmal aber kann er sich auf die inzwischen entwickelte lokale Klassenkörpertheorie in ihrer lokalen Begründung stützen; diese wurde von Chevalley und Herbrand besonders vereinfacht. Hasse zitiert dazu die Chevalleysche Thèse [Che33b], die in derselben Zeitschrift unmittelbar vor der Hasseschen Arbeit abgedruckt ist. Obwohl, wie gesagt, Hasse die Artinsche Frage hier nicht löst, so ist [Has34b] im abelschen Fall als eine Vereinfachung und Systematisierung der Resultate aus [Has30d] zu werten.
Cahit Arf war ein Doktorand von Hasse in den Jahren 1937–1938 in Göttingen. Offenbar erinnerte sich Hasse an das damalige Desideratum von Artin, dass die Theorie der Führer ohne Benutzung der Klassenkörpertheorie begründet werden sollte. Daher stellte er Arf die Aufgabe, nach einer solchen Begründung zu suchen. Es geht darum, die Gültigkeit der Hasseschen Formel (46) mit den Kongruenzen (47) für eine abelsche Erweiterung K|k eines beliebigen diskret bewerteten kompletten Körpers k mit vollkommenem Restklassenkörper zu beweisen. Es genügt, den rein verzweigten Fall zu behandeln; man kann sich dabei auf den zyklischen Fall beschränken. Arf führte das in seiner Dissertation [Arf39] durch; wir haben diese Arbeit bereits in 32.2 erwähnt.
Interessant ist, dass Arf als Hilfsmittel die Einbettung von K|k in nichtkommutative Algebren A betrachtet, und zwar so, dass die Hauptordnung von K in einer Maximalordnung von A enthalten ist. Er benutzt dabei, erstens, die von Hasse [Has31b] entwickelte Strukturtheorie der lokalen Algebren, und zweitens, den Zusammenhang zwischen den Hauptordnungen einer lokalen Divisionsalgebra mit denen ihrer maximalen Teilkörper, wie sie von Hasse in dem Herbrand-Gedächtnisband dargestellt worden war [Has34d]. (Hierzu siehe auch Noether [Noe34]; die sich überschneidenden Noetherschen und Hasseschen Resultate sind unabhängig voneinander gefunden worden.) Die Heranziehung von nicht-kommutativen Algebren erinnert an den Ansatz von Emmy Noether in [Noe32], die ja ebenfalls die Artinschen Führer mit Hilfe nicht-kommutativer Strukturen gewinnen wollte.
Die Arbeit von Arf ist nicht einfach zu lesen. Uns scheint, dass sie in weiten Teilen im Stil von Marc Krasner geschrieben wurde. Das erklärt sich vielleicht dadurch, dass Arf in Paris studiert hatte, bevor er nach Göttingen kam. Ein Teil seiner Techniken und Hilfsbetrachtungen über die Erzeugung rein verzweigter Erweiterungen wurden unabhängig auch von Krasner in [Kra37] entwickelt. Arf hatte diese Arbeit im Zentralblatt für Mathematik referiert.
Der von Arf bewiesene Satz wird heute allgemein als „Satz von Hasse-Arf“ bezeichnet. Hasse hatte diesen Satz für die lokalen Körper in der Zahlentheorie bewiesen; das läuft auf den Fall endlicher Restklassenkörper zurück. Die Verallgemeinerung von Arf besteht darin, dass er beliebige vollkommene Restklassenkörper zulässt und damit die Beweise unabhängig von der Klassenkörpertheorie führt.
In Weiterführung und Vereinfachung der Arfschen Untersuchungen [Arf39] sind folgende Arbeiten zu nennen:
Serre [Ser61] hat für diskret bewertete komplette Körper mit algebraisch abgeschlossenem Restklassenkörper eine Art Klassenkörpertheorie entwickelt, und in diesem Rahmen den Satz von Hasse-Arf bewiesen. Der Fall eines beliebigen vollkommenen Restklassenkörpers kann darauf zurückgeführt werden.
In seinem Buch „Corps locaux“ [Ser62] hat Serre die Hassesche Normenresttheorie auf den Fall eines beliebigen (vollkommenen) Restklassenkörpers erweitert. Als Anwendung wird dann der Satz von Hasse-Arf in diesem Rahmen bewiesen. Dabei (wie auch in der vorgenannten Arbeit) wird alles auf den Fall einer rein verzweigten zyklischen Erweiterung von p-Potenzgrad reduziert; dies ist also das Kernstück des Beweises. Es verwundert, dass nicht Hasse selbst im Anschluss an seine Normenresttheorie aus [Has34b] auf diese, von der (lokalen) Klassenkörpertheorie unabhängige Beweisvariante gekommen ist.
Im Jahr 1969 hat Shankar Sen, ein Doktorand von Tate, einen besonders einfachen und schönen Beweis des Satzes von Hasse-Arf gegeben. Zwar ist dieser Beweis auf rein verzweigte zyklische Erweiterungen von p-Potenzgrad beschränkt, aber wir haben schon oben erwähnt, dass dieser Satz das Kernstück des Beweises für beliebige abelsche Erweiterungen bildet. Sen zeigt, dass in diesem Falle die Kongruenzen
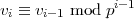
gelten; dies sind in der Tat die Kongruenzen (47) im zyklischen Falle.
Für weitere Informationen siehe [Roq00].