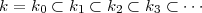
Offenbar hatte Hasse gefragt, was Artin zum Klassenkörperturmproblem meine.
Das Klassenkörperturmproblem war von Hasse in Teil I seines Klassenkörperberichtes [Has26a] als ein ungelöstes Problem der Klassenkörpertheorie aufgeführt worden. Es sei k = k0 ein Zahlkörper und sukzessiv ki der Hilbertsche Klassenkörper von ki-1. Man erhält einen Körperturm
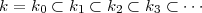
und es entsteht das Problem, zu entscheiden, ob dieser Turm immer abbricht. Wenn ja, dann bedeutet das, dass k in einen unverzweigten Körper mit der Klassenzahl 1 eingebettet werden kann; das wäre, so sagt Hasse, ein gewisses Seitenstück zum Hauptidealsatz.
Hasse schreibt in seinem Bericht, dass dieses Problem von Furtwängler aufgeworfen worden sei, und er bezieht sich dabei auf eine mündliche Mitteilung von Artin. Allerdings schreibt Furtwängler dazu in einem Brief an Hasse vom 23.6.1926:
„…Ich möchte noch eine kurze Bemerkung über Ihren schönen Bericht hinzufügen. Die Angabe über eine Mitteilung des Herrn Artin bezüglich des Klassenkörperturmes dürfte auf einer Verwechslung mit Herrn Dr.Schreier beruhen, mit dem ich öfter über diese Dinge gesprochen habe.“
Das bedeutet anscheinend, dass die Problemstellung von Schreier stammt, und dass Furtwängler dies aus seinen Gesprächen mit Schreier übernommen hatte.
Interessant ist, dass Artin dieses Turmproblem von vorneherein nicht als
gruppentheoretisches Problem ansieht, während er doch beim Hauptidealsatz
davon überzeugt war, dass dieser auf ein rein gruppentheoretisches Problem
zurückläuft, was er schon im Brief Nr.13 vom 2.August zum Ausdruck gebracht
hatte. Beides hat sich bewahrheitet: Einerseits bewies Furtwängler 1928 den
Hauptidealsatz mit Hilfe eines gruppentheoretischen Satzes, der aufgebaut war
auf der von Artin und Schreier ausgearbeiteten Verlagerungstheorie (siehe 13.1.1).
Andererseits konnte schließlich nachgewiesen werden, dass die von Artin in
seinem Brief beschriebenen unendlichen Folgen  1,
1, 2,… von Gruppen
wirklich existieren, und dass es auf die spezielle arithmetische Struktur des
Grundkörpers ankommt, ob der Klassenkörperturm endlich oder unendlich
ist.
2,… von Gruppen
wirklich existieren, und dass es auf die spezielle arithmetische Struktur des
Grundkörpers ankommt, ob der Klassenkörperturm endlich oder unendlich
ist.
Die von Artin erwähnte „Verschärfung der Minkowskischen Abschätzung“ findet sich bereits in Teil I des Hasseschen Klassenkörperberichtes [Has26a] erwähnt, nämlich: Es handelt sich um die Minkowskische Abschätzung des Diskriminantenbetrages |d| eines Zahlkörpers. Danach ist
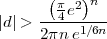 | (30) |
wobei n der Grad des in Rede stehenden Zahlkörpers ist. Könnte diese
Abschätzung auf der rechten Seite verschärft werden durch die n-te Potenz irgend
einer gegen +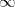 strebenden Funktion als Faktor, also etwa (log n)n oder
(log log n)n…, so könnte aus dieser verschärften Abschätzung, angewandt auf
einen hinreichend hohen Körper des Klassenkörperturms, geschlossen werden,
dass der Klassenkörperturm stets abbricht. Das ist die Artinsche Idee, die Hasse
in seinem Bericht [Has26a] ausführt.
strebenden Funktion als Faktor, also etwa (log n)n oder
(log log n)n…, so könnte aus dieser verschärften Abschätzung, angewandt auf
einen hinreichend hohen Körper des Klassenkörperturms, geschlossen werden,
dass der Klassenkörperturm stets abbricht. Das ist die Artinsche Idee, die Hasse
in seinem Bericht [Has26a] ausführt.
Wie wir aus diesem Brief entnehmen, hält Artin dies immer noch für den aussichtsreichsten Beweisansatz, um die Endlichkeit des Klassenkörperturms zu beweisen. Es ist allerdings nicht klar, ob Artin meint, dass der Klassenkörperturm stets endlich ist, also für einen beliebigen Zahlkörper als Grundkörper, oder ob er bereits die Möglichkeit in Betracht zieht, dass der Klassenkörperturm manchmal endlich und auch manchmal unendlich sein kann, je nach der „speziellen arithmetischen Natur des Grundkörpers“, wie er sich ausdrückt. Wir neigen dazu, anzunehmen, dass Artin die letztere Möglichkeit meint, die sich dann ja auch in der Folge bewahrheitet hat.
Nachstehend geben wir einen Überblick über die weitere Entwicklung zum Klassenkörperturmproblem.
Wir haben Arnold Scholz bereits in 12.1.4 erwähnt. Scholz (1904-1942) hatte bei I.Schur in Berlin studiert. Er pflegte schon als junger Student einen regen Briefwechsel mit Hasse, der erst mit Scholz’ Tod 1942 endete; insgesamt enthält der Nachlass von Hasse mehr als 100 Briefe von und an Scholz, vollgepackt mit Mathematik.
Im Oktober 1928 teilte Scholz in einem Brief an Hasse mit, dass und wie er
Zahlkörper mit beliebig großem Klassenkörperturm konstruieren könne. Hasse
informierte Artin sofort über dieses Resultat; wir schließen das daraus, dass sich
Artin in seinem Brief Nr.20 vom 14.11.1928 dafür bedankt. Für die Einzelheiten
der Scholzschen Konstruktion, die 1929 im Crelleschen Journal erschien, verweisen
wir auf 20.1.1. Demnach wusste Artin spätestens zu diesem Zeitpunkt, dass es
beliebig hohe Klassenkörpertürme gibt, auch für Grundkörper vom Primzahlgrad
 . Allerdings blieb die Frage offen, ob ein Klassenkörperturm unendlich sein
kann.
. Allerdings blieb die Frage offen, ob ein Klassenkörperturm unendlich sein
kann.
In Hasses Tagebuch haben wir eine Eintragung aus späterer Zeit gefunden, datiert im „Februar 1934“, mit dem Titel:
Konstruktion von Körpern mit beliebig hohem Klassenkörperturm (nach Artin).
In der ersten Februarwoche 1934 hatte Hasse auf Einladung von Artin in Hamburg eine Vortragsserie gehalten, über seinen neuen Beweis der Riemannschen Vermutung für elliptische Funktionenkörper mit endlichem Konstantenkörper (vgl. Brief Nr.48). Die in Rede stehende Tagebucheintragung beruht offenbar auf einem bei dieser Gelegenheit geführten Gespräch Hasses mit Artin. Sie zeigt uns, dass Artin sich 1934 immer noch mit dem Klassenkörperturmproblem beschäftigte.
Die Artinsche Konstruktion ist so einfach, dass wir die Hassesche Eintragung nachstehend wörtlich wiedergeben, insbesondere weil sie niemals publiziert wurde und ganz unbekannt ist.
Zu jeder
gegebenen endlichen Gruppe G kann man einen algebraischen
Zahlkörper k mit einem galoisschen Relativkörper K|k der Gruppe
G konstruieren. Seien  1,…,
1,…, n die Diskriminantenprimteiler von
K|k. Dann sind die zugehörigen Körper K
n die Diskriminantenprimteiler von
K|k. Dann sind die zugehörigen Körper K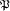 i metazyklisch. Man
kann nun einen zu K|k fremden Körper k so konstruieren,
dass seine Lokalisierungen für die Stellen
i metazyklisch. Man
kann nun einen zu K|k fremden Körper k so konstruieren,
dass seine Lokalisierungen für die Stellen  i mit den K
i mit den K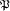 i
übereinstimmen. Dann ist Kk|k unverzweigt mit der Gruppe
G. So kann man Körper von beliebig hohem Klassenkörperturm
konstruieren.
i
übereinstimmen. Dann ist Kk|k unverzweigt mit der Gruppe
G. So kann man Körper von beliebig hohem Klassenkörperturm
konstruieren.
Der letzte Satz ist offenbar so zu interpretieren, dass durch geeignete Wahl der Gruppe G der Klassenkörperturm von k beliebig groß wird. In der Tat: wenn G metabelsch von der Stufe n ist, dann ist Kk im n-ten Klassenkörper von k enthalten.
Einen Hilfskörper k im angegebenen Sinne kann man ganz elementar finden,
unter Benutzung des Henselschen Lemmas: Sei fi(X) ein definierendes Polynom
von K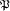
 über k
über k i; sein Grad ist ni = [K
i; sein Grad ist ni = [K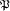 i : k
i : k i]. Es bedeute n das kleinste
gemeinsame Vielfache der ni. Man approximiere nun die Polynome fi(X)n/ni
simultan durch ein Polynom g(X)
i]. Es bedeute n das kleinste
gemeinsame Vielfache der ni. Man approximiere nun die Polynome fi(X)n/ni
simultan durch ein Polynom g(X)  k[X] vom Grad n. Dann nehme man
k als den Körper einer Nullstelle von g(X); wenn die Approximation
hinreichend gut ist so zerfällt g(X) über k
k[X] vom Grad n. Dann nehme man
k als den Körper einer Nullstelle von g(X); wenn die Approximation
hinreichend gut ist so zerfällt g(X) über k
 als die n/ni-te Potenz eines über
k
als die n/ni-te Potenz eines über
k i irreduziblen Polynoms, welches denselben Körper K
i irreduziblen Polynoms, welches denselben Körper K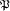 i erzeugt wie
fi(X).
i erzeugt wie
fi(X).
Die Artinsche Konstruktion unverzweigter Körper ist aber nicht nur für das Klassenkörperturmproblem von Interesse. Denn ein Klassenkörperturm liefert ja stets metazyklische Galoisgruppen, während hier gezeigt wird, dass jede endliche Gruppe als Galoisgruppe eines relativ unverzweigten Zahlkörpers auftritt. Wir wissen aus einem späteren Brief, dass Artin darüber sehr erstaunt war; vgl. Brief Nr.37 vom 6.5.1931. Bis dahin hatte Artin nicht geglaubt, dass „es überhaupt einen unverzweigten, nicht metazyklischen Körper gibt.“
Im weiteren wurde versucht, unabhängig vom Klassenkörperturmproblem,
also auf rein gruppentheoretischem Wege, das von Artin aufgeworfene
gruppentheoretische Turmproblem zu lösen, nämlich ob es beliebig lange (oder
gar unendliche) Folgen endlicher nichttrivialer Gruppen 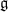 1,
1,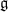 2,… gibt derart, dass
2,… gibt derart, dass
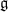 i-1 die Faktorgruppe der (i- 1)-ten Kommutatorgruppe von
i-1 die Faktorgruppe der (i- 1)-ten Kommutatorgruppe von 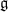 i ist. Wir sprechen
dann kurz von „Gruppentürmen“. Und zwar sucht man nach solchen großen
Türmen, deren erstes Glied
i ist. Wir sprechen
dann kurz von „Gruppentürmen“. Und zwar sucht man nach solchen großen
Türmen, deren erstes Glied 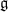 1 (also die Faktorkommutatorgruppe) eine
vorgegebene abelsche Gruppe G ist. Mit der letztgenannten Bedingung geht die
Problemstellung über die in dem vorliegenden Brief aufgeworfene Frage von Artin
hinaus, denn Artin spricht nicht davon, dass die Faktorkommutatorgruppe
vorgegeben sein soll. Die von Scholz konstruierten großen Türme (über die wir in
15.1.2 berichteten) sind dafür nicht geeignet, da die Faktorkommutatorgruppe
(also die Idealklassengruppe des Grundkörpers) mit der Höhe des Turmes
wächst.
1 (also die Faktorkommutatorgruppe) eine
vorgegebene abelsche Gruppe G ist. Mit der letztgenannten Bedingung geht die
Problemstellung über die in dem vorliegenden Brief aufgeworfene Frage von Artin
hinaus, denn Artin spricht nicht davon, dass die Faktorkommutatorgruppe
vorgegeben sein soll. Die von Scholz konstruierten großen Türme (über die wir in
15.1.2 berichteten) sind dafür nicht geeignet, da die Faktorkommutatorgruppe
(also die Idealklassengruppe des Grundkörpers) mit der Höhe des Turmes
wächst.
Das Problem wird etwas einfacher, wenn man p-Türme betrachtet, also solche
Türme, bei denen die Gruppen 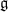 i p-Gruppen sind, wobei p eine Primzahl
bedeutet. Und entsprechend p-Klassenkörpertürme.
i p-Gruppen sind, wobei p eine Primzahl
bedeutet. Und entsprechend p-Klassenkörpertürme.
Im Jahre 1935 publizierte Magnus eine Arbeit [Mag35], in welcher er eine neue
Methode präsentierte, um mit Gruppen zu arbeiten, die durch Erzeugende und
definierende Relationen gegeben sind. Sozusagen als Nebenprodukt stellt er fest,
dass es für p = 3 beliebig große 3-Gruppentürme gibt, deren erstes Glied 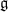 1
eine abelsche Gruppe vom Typ (3,3,3) ist, also direktes Produkt von
drei zyklischen Gruppen der Ordnung 3. Dieses Ergebnis, obwohl rein
gruppentheoretisch, wurde sofort registriert als relevant für die Untersuchung
der Klassenkörpertürme: das wurde sowohl im Zentralblatt-Referat (von
Olga Taussky) als auch im Referat des „Jahrbuch für die Fortschritte der
Mathematik“ (von Arnold Scholz) betont. Es scheint jedoch nicht klar zu sein,
ob es gelingt, mit dieser Methode auch unendliche Gruppentürme zu
bauen.
1
eine abelsche Gruppe vom Typ (3,3,3) ist, also direktes Produkt von
drei zyklischen Gruppen der Ordnung 3. Dieses Ergebnis, obwohl rein
gruppentheoretisch, wurde sofort registriert als relevant für die Untersuchung
der Klassenkörpertürme: das wurde sowohl im Zentralblatt-Referat (von
Olga Taussky) als auch im Referat des „Jahrbuch für die Fortschritte der
Mathematik“ (von Arnold Scholz) betont. Es scheint jedoch nicht klar zu sein,
ob es gelingt, mit dieser Methode auch unendliche Gruppentürme zu
bauen.
1958 publizierte Olga Taussky-Todd [Tau58] als Research Problem die Aufgabe, zu gegebener abelscher p-Gruppe G die Höhe von Gruppentürmen abzuschätzen, die mit G als Faktorkommutatorgruppe beginnen. 1970 zeigte Serre [Ser70], dass es stets unendliche Gruppentürme dieser Art gibt, ausgenommen die Fälle, die schon Taussky bekannt waren, nämlich wenn G zyklisch ist oder eine 2-Gruppe vom Typus (2,2).124 Damit wurde also die Frage von Artin-Taussky im gruppentheoretischen Sinn beantwortet.
Die Serresche Konstruktion ist im Rahmen der pro-p-Gruppen einfach und
übersichtlich: Wenn nicht einer der Ausnahmefälle vorliegt, so lässt sich
G = A×B als direktes Produkt zweier nichttrivialer abelscher p-Gruppen A und
B darstellen, wobei mindestens eine, etwa A, eine Ordnung |A| > 2 besitzt,
während jedenfalls |B|> 2. Sei A * B das freie Produkt in der Kategorie der
p-Gruppen. Der Kern R des natürlichen Homomorphismus A * B  A × B
ist gleich der Kommutatorgruppe von A * B und wird erzeugt von den
Kommutatoren [a,b] mit a
A × B
ist gleich der Kommutatorgruppe von A * B und wird erzeugt von den
Kommutatoren [a,b] mit a  A,b
A,b  B und a,b≠1. Und zwar ist R die freie
pro-p-Gruppe mit diesen Erzeugenden. Deren Anzahl ist > 1 und somit ist die
absteigende Kommutator-Reihe unendlich.
B und a,b≠1. Und zwar ist R die freie
pro-p-Gruppe mit diesen Erzeugenden. Deren Anzahl ist > 1 und somit ist die
absteigende Kommutator-Reihe unendlich.
Im Jahre 1964 erschien die Arbeit [GS64] von Golod und Shafarevich mit dem Ergebnis, dass es unendliche Klassenkörpertürme gibt. Das kam ziemlich überraschend, nicht weil man die Endlichkeit der Klassenkörper-Türme erwartete, sondern weil man bis dahin keine Möglichkeit sah, an das Problem heranzukommen. Diese Arbeit liefert eine glänzende Bestätigung für die Artinsche Vision im vorliegenden Brief, nämlich dass „erst die spezielle arithmetische Natur des Grundkörpers hier den Ausschlag geben“ wird. In der Tat wird in der Arbeit gezeigt, dass der Klassenkörperturm unendlich ist, wenn der Rang der Idealklassengruppe hinreichend groß ist.
Genauer gesagt, geht es um p-Klassenkörpertürme für eine vorgegebene Primzahl p. Gegeben sei ein Zahlkörper k vom Grad n. Ferner sei dp der p-Rang seiner Idealklassengruppe. Aus den Resultaten von Golod-Shafarevich ergibt sich: Wenn
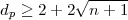 | (31) |
so ist der p-Klassenkörperturm über k unendlich. (Siehe dazu auch [Roq67] und [RZ69].) Und zwar ist diese arithmetische Bedingung die Folge einer gruppentheoretischen Bedingung im Rahmen der pro-p-Gruppen, nämlich wie folgt:
Nach der Klassenkörpertheorie ist dp der Rang der Galoisgruppe G des
Hilbertschen p-Klassenkörpers, und diese ist die Kommutator-Faktorgruppe der
Galoisgruppe 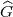 des gesamten p-Klassenkörperturms. Also ist dp auch der Rang
der pro-p-Gruppe
des gesamten p-Klassenkörperturms. Also ist dp auch der Rang
der pro-p-Gruppe 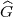 , d.h. die Minimalanzahl der Erzeugenden von
, d.h. die Minimalanzahl der Erzeugenden von 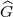 . Es sei rp
die Minimalanzahl der Relationen zwischen diesen Erzeugenden, d.h. der
Rang der Relationengruppe. Nach Golod und Shafarevich bedingt die
gruppentheoretische Ungleichung
. Es sei rp
die Minimalanzahl der Relationen zwischen diesen Erzeugenden, d.h. der
Rang der Relationengruppe. Nach Golod und Shafarevich bedingt die
gruppentheoretische Ungleichung
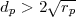 | (32) |
dass die pro-p-Gruppe 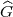 unendlich ist. In einer endlichen p-Gruppe gibt
es also relativ viele Relationen, mehr als die angegebene Ungleichung
erlaubt.
unendlich ist. In einer endlichen p-Gruppe gibt
es also relativ viele Relationen, mehr als die angegebene Ungleichung
erlaubt.
Der Übergang von (32) zu (31) wird geliefert durch eine Abschätzung der Relationenanzahl rp im Vergleich zu arithmetischen Invarianten des Körpers k, insbesondere zum Rang der Einheitengruppe. Diese Abschätzung beruht auf der kohomologischen Deutung der Klassenkörpertheorie im Sinne der Theorie von Artin und Tate [AT68], die Anfang der 1950er Jahre im Seminar von Artin in Princeton entwickelt worden war. Die Methoden dafür waren zur Zeit des vorliegenden Briefes, also 1927, noch nicht verfügbar. Immerhin ist es interessant, dass Artin die Methoden der kohomologischen Algebra, die in den 1930er Jahren im Entstehen begriffen war, im Hinblick auf Anwendungen in der Klassenkörpertheorie schon damals vorangetrieben hat. Das geht aus späteren Briefen von Artin an Hasse hervor.
Für quadratische Körper (n = 2) liefert (31) die Bedingung dp > 5. Durch
Verfeinerung der Methoden konnten Koch und Venkov [KV75] zeigen, dass für
quadratische Körper sogar dp > 2 ausreicht, damit der p-Klassenkörperturm
unendlich ist, jedenfalls für ungerade Primzahlen p. Das ist interessant, weil
schon früher (1934) Arnold Scholz und Olga Taussky [ST34] Beispiele
quadratischer Körper mit 3-Klassengruppe vom Rang 2 und endlichem
3-Klassenkörperturm angegeben hatten. Wenn p = 2 ist, dann geht es um den
2-Rang d2 der 2-Klassengruppe eines quadratischen Zahlkörpers. Die
Geschlechtertheorie von Gauss liefert bekanntlich Idealklassengruppen von
beliebig großem Rang, abhängig von der Anzahl der Diskriminantenteiler;
danach ist es leicht, numerische Beispiele von quadratischen Körpern
mit unendlichem Klassenkörperturm anzugeben. Golod und Shafarevich
nennen z.Bsp.  (
(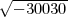 ). Unter Ausnutzung weiterer arithmetischer
Eigenschaften des Körpers lassen sich jedoch noch numerisch kleinere Beispiele
finden.
). Unter Ausnutzung weiterer arithmetischer
Eigenschaften des Körpers lassen sich jedoch noch numerisch kleinere Beispiele
finden.