6.4 Kubische Gauss’sche Summen
Artin benutzt die Terminologie „Lagrangesche Wurzelzahlen“, die auch Hilbert
in seinem Zahlbericht [Hil97] verwendet. Heute spricht man wohl meist von
„Gauss’schen Summen“.
Bei dem Beweis des Eisensteinschen Reziprozitätsgesetzes für Einheitswurzeln
von Primzahlordnung  spielen die Gauss’schen Summen eine wichtige
Rolle. Dies erklärt, warum Artin jetzt sagt, auch für höhere Exponenten
spielen die Gauss’schen Summen eine wichtige
Rolle. Dies erklärt, warum Artin jetzt sagt, auch für höhere Exponenten
 n laufe das Eisensteinsche Reziprozitätsgesetz wieder auf Gauss’sche
Summen (oder Lagrangesche Wurzelzahlen) hinaus, aber diesmal eben für
Einheitswurzeln von höherer Ordnung
n laufe das Eisensteinsche Reziprozitätsgesetz wieder auf Gauss’sche
Summen (oder Lagrangesche Wurzelzahlen) hinaus, aber diesmal eben für
Einheitswurzeln von höherer Ordnung  n. Das sei, so Artin, ungleich
schwieriger.
n. Das sei, so Artin, ungleich
schwieriger.
Weshalb er sich dann jedoch ausgerechnet mit kubischen Gauss’schen
Summen beschäftigt, also mit  = 3, ist in diesem Zusammenhang nicht ganz
einsichtig. Wahrscheinlich war es das wichtige und tiefliegende, im quadratischen
Falle auf Gauss zurückgehende Problem der „Vorzeichenbestimmung“, das im
kubischen Falle noch nicht gelöst war, was Artin gereizt hat, sich damit zu
beschäftigen. Im kubischen Fall geht es nicht um das Vorzeichen, sondern um den
Winkelsextanten, in den eine Gauss’sche Summe fällt. Für den Beweis des
Eisensteinschen Reziprozitätsgesetzes spielt das zwar keine Rolle, denn dort geht
es nach den üblichen Beweisen um die
= 3, ist in diesem Zusammenhang nicht ganz
einsichtig. Wahrscheinlich war es das wichtige und tiefliegende, im quadratischen
Falle auf Gauss zurückgehende Problem der „Vorzeichenbestimmung“, das im
kubischen Falle noch nicht gelöst war, was Artin gereizt hat, sich damit zu
beschäftigen. Im kubischen Fall geht es nicht um das Vorzeichen, sondern um den
Winkelsextanten, in den eine Gauss’sche Summe fällt. Für den Beweis des
Eisensteinschen Reziprozitätsgesetzes spielt das zwar keine Rolle, denn dort geht
es nach den üblichen Beweisen um die  -te Potenz der Gausschen Summe.
Aber für sich genommen ist die Vorzeichenbestimmung ein interessantes
Problem.
-te Potenz der Gausschen Summe.
Aber für sich genommen ist die Vorzeichenbestimmung ein interessantes
Problem.
Dieses von Artin angesprochene Problem ist alt und wurde von Kummer in
den Jahren 1842-1846 im Crelleschen Journal gestellt. Nur aus dem vorliegenden
Brief weiß man, dass sich Artin damit beschäftigt hat; in den Publikationen von
Artin erscheint das Problem nicht.
Um den von Artin als Beilage beigefügten Zettel zu lesen, beachte man, dass
in seiner Bezeichnungsweise R den Körper der rationalen Zahlen bedeutet, und 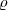 die analytisch normierte primitive dritte Einheitswurzel. Ferner bezeichnet
die analytisch normierte primitive dritte Einheitswurzel. Ferner bezeichnet 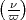 den normierten kubischen Charakter modulo einer Primzahl
den normierten kubischen Charakter modulo einer Primzahl  von R(
von R(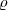 ), definiert
durch die Kongruenz
), definiert
durch die Kongruenz
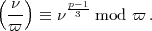
Dabei ist  derjenige von den beiden Teilern von p, der normiert ist wie in der Artinschen
Beilage angegeben.
Mit S(
derjenige von den beiden Teilern von p, der normiert ist wie in der Artinschen
Beilage angegeben.
Mit S( ) bezeichnet Artin die zugehörige Gauss’sche Summe. Das Kummersche
Problem besteht darin, herauszufinden, wie groß der Anteil derjenigen
Primzahlen p ist, für welche S(
) bezeichnet Artin die zugehörige Gauss’sche Summe. Das Kummersche
Problem besteht darin, herauszufinden, wie groß der Anteil derjenigen
Primzahlen p ist, für welche S( ) in einen bestimmten Winkelsextanten
fällt, oder, damit gleichbedeutend, für welche eine bestimmte Anordnung
für die reellen Zahlen
) in einen bestimmten Winkelsextanten
fällt, oder, damit gleichbedeutend, für welche eine bestimmte Anordnung
für die reellen Zahlen  0,
0, 1,
1, 2 vorliegt (in der Bezeichnungsweise von
Artin).
2 vorliegt (in der Bezeichnungsweise von
Artin).
Es erscheint bemerkenswert, dass Artin auf dem Zettel, den er dem Brief an
Hasse beilegt, das Kummersche Problem ausführlich beschreibt, unter Beifügung
der Tabellen von Kummer. Diese Beilage enthält eigentlich nur das, was ohnehin
bekannt war, abgesehen vielleicht von den Tabellen für A und B, die
aber ganz elementar zu berechnen sind. Hatte Artin angenommen, dass
Hasse das Kummersche Problem nicht kannte? Das Problem wird doch im
Hilbertschen Zahlbericht zumindest erwähnt, und der Zahlbericht war Artin und
Hasse wohlbekannt. Vielleicht hatte Artin die Tabellen von Kummer
nachgerechnet und wollte nunmehr Hasse das Ergebnis seiner Rechnungen
präsentieren? Das erscheint allerdings unwahrscheinlich. Wie uns Prof. S.
Patterson schreibt „sind die Summen mit der Hand etwas unangenehm zu
berechnen, weil man mit langen Dezimalzahlen arbeiten muss“. Patterson fährt
fort:
Ich nehme an, dass er [Artin] die Werte der kubischen
Summen nicht nachgerechnet hat - er hat die Primzahlen p  1 mod 6 von Kummer übernommen und die Werte von A und
B nachgerechnet. Er behauptet ja auch nicht, dass er alles
nachgerechnet hat. Kummer listet die Primzahlen p zu den drei
Klassen auf. Ich nehme an, dass Artin versucht hat, diese zu
interpretieren, um die Beobachtungen von Kummer mit den
Sätzen von Frobenius (und ggfs. Tschebotareff ) zu erklären. Es
ist ihm natürlich nicht gelungen, aber dies war von vornherein
nicht klar.
1 mod 6 von Kummer übernommen und die Werte von A und
B nachgerechnet. Er behauptet ja auch nicht, dass er alles
nachgerechnet hat. Kummer listet die Primzahlen p zu den drei
Klassen auf. Ich nehme an, dass Artin versucht hat, diese zu
interpretieren, um die Beobachtungen von Kummer mit den
Sätzen von Frobenius (und ggfs. Tschebotareff ) zu erklären. Es
ist ihm natürlich nicht gelungen, aber dies war von vornherein
nicht klar.
Ich glaube nicht, dass Artin sich öffentlich zu dem
Kummer-Problem geäussert hat. Das Problem fand im späten
19.Jh. und frühen 20.Jh. in der Literatur wenig Beachtung. Es
gab überhaupt keine Methoden – sogar die klassischen Methoden
der analytischen Zahlentheorie wurden erst gegen 1900 etabliert.
Auch Hilbert geht nicht darauf ein, obwohl er die Arbeiten von
Kummer zitiert. Mein Eindruck ist, dass Hasse derjenige war,
der die Aufmerksamkeit der Zahlentheorie-Gemeinde auf dieses
Problem gelenkt hat.
In der Tat hat Hasse später, im Jahre 1950, das Kummersche Problem ausführlich
dargestellt, nämlich in seinem Buch „Vorlesungen über Zahlentheorie“
[Has50]. Dort berichtet er über das von Kummer an seinem numerischen
Material gefundene Verhältnis 3 : 2 : 1 das Artin in seinem Brief als
„rätselhaft“ bezeichnet, und er stellt fest, dass sich dieses Verhältnis auch in
den Primzahl-Zerlegungstypen der nichtabelschen, kubischen Zahlkörper
findet. Jedoch hält Hasse es nicht für wahrscheinlich, dass es sich bei der
Kummerschen Klasseneinteilung um die Widerspiegelung eines Zerlegungsgesetzes
handelt. Jedenfalls bezeichnet Hasse in seinem Buch „die Inangriffnahme der
Kummerschen Vermutung als eine lohnende, reizvolle Aufgabe.“
Die Lösung des Kummerschen Problems wurde erst 1979 von Heath-Brown
und Patterson gefunden [HBP79]. Und zwar anders, als es die numerischen
Experimente von Kummer suggerieren. Statt des Verhältnisses 3 : 2 : 1 stellte sich
nunmehr heraus, dass in Wahrheit Gleichverteilung vorliegt.
 spielen die Gauss’schen Summen eine wichtige
Rolle. Dies erklärt, warum Artin jetzt sagt, auch für höhere Exponenten
spielen die Gauss’schen Summen eine wichtige
Rolle. Dies erklärt, warum Artin jetzt sagt, auch für höhere Exponenten
 n laufe das Eisensteinsche Reziprozitätsgesetz wieder auf Gauss’sche
Summen (oder Lagrangesche Wurzelzahlen) hinaus, aber diesmal eben für
Einheitswurzeln von höherer Ordnung
n laufe das Eisensteinsche Reziprozitätsgesetz wieder auf Gauss’sche
Summen (oder Lagrangesche Wurzelzahlen) hinaus, aber diesmal eben für
Einheitswurzeln von höherer Ordnung  n. Das sei, so Artin, ungleich
schwieriger.
n. Das sei, so Artin, ungleich
schwieriger.
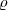
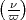 den normierten kubischen Charakter modulo einer Primzahl
den normierten kubischen Charakter modulo einer Primzahl