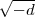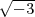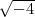47.1 Der Fehler beim Hauptidealsatz

Es handelt sich um die Hassesche Arbeit „Zum Hauptidealsatz in der komplexen Multiplikation“ in den Monatsheften der Mathematik und Physik 1931 [Has31c]. Es geht um einen Beweis des Hauptidealsatzes für die Klassenkörper der imaginär-quadratischen Körper. Ein solcher Beweis war im Jahre 1929 in der Dissertation von W.Schäfer gegeben worden, einem Doktoranden Hasses. Zwar war 1929 schon ein allgemeiner Beweis des Hauptidealsatzes im Rahmen der Klassenkörpertheorie bekannt, und zwar nach Furtwängler (vgl. 13.1.3). Jedoch strebte Hasse einen auf analytischen Grundlagen fußenden Beweis im Rahmen der komplexen Multiplikation an (vgl. 6.1).

Schäfers Beweis war jedoch noch mit einigen Zusatzbedingungen belastet; er konnte nur solche Primideale behandeln, die nicht in der Diskriminante des imaginär-quadratischen Körpers k aufgehen und deren Norm N 1 mod 12 ist. In einem zweiten Beweis konnte er zwar alle Primideale behandeln, musste aber voraussetzen, dass die Diskriminante d prim ist zu 2 und 3. Die Schäfersche Dissertation [Sch29a] ist niemals in einer mathematischen Zeitschrift publiziert worden. Sie war jedoch als gedruckte Dissertation erhältlich und es ist anzunehmen, dass Artin ein Exemplar davon erhalten hatte.

Ausgehend von der Schäferschen Dissertation hatte Hasse im Jahre 1931 einen Beweis publiziert, der die von Schäfer ausgelassenen Fälle mit behandelt [Has31c]. Wie wir aus diesem Brief entnehmen, hatte Artin nun einen Fehler bemerkt, der sowohl die Schäfersche als auch die Hassesche Arbeit betrifft.

Wie es scheint, konnte dieser Fehler nicht sofort beseitigt werden. Hasse ist auf diese Frage später noch einmal zurückgekommen, in der Arbeit „Zur Geschlechtertheorie in quadratischen Zahlkörpern“ 1951 im Journal of the Mathematical Society of Japan [Has51b]. Dort heißt es:

Dabei bezieht sich Hasse auf die oben genannte Arbeit [Has31c].

Wie Artin in seinem Brief erläutert, geht es darum, ob in jeder Idealklasse des gegebenen imaginär-quadratischen Zahlkörpers k = (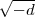) Ideale mit Norm N 1 mod 12 vorkommen. Das ist jedoch nicht immer der Fall. Hasse zeigt nun in [Has51b], dass dies dann und nur dann der Fall ist, wenn der absolute Klassenkörper linear disjunkt ist zum Körper k(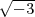,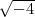), d.h. wenn die Primdiskriminanten -3,-4 nicht als Diskriminantenprimteiler von k vorkommen. Für die hierdurch nicht erfassten imaginär-quadratischen Körper ist daher die Hasse-Schäfersche Methode nicht anwendbar. Kurz darauf hat Terada [Ter54] gezeigt, dass durch eine Modifikation des Hasseschen Beweises auch die Klassen von Idealen mit N() 5 mod 12 erfasst werden können. Schliesslich hat dann Reichardt [Rei59] einen ausnahmslos gültigen Beweis gegeben.