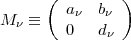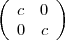47 02.12.1932, Brief von Artin an Hasse
2.12.32
Lieber Herr Hasse!
Eine unangenehme Nachricht. In der Arbeit von Herrn Schäfer und auch in
der Ihren findet sich eine Unrichtigkeit, so dass der Hauptidealsatz im
Rahmen der kompl[exen] Multipl[ikation] noch immer nicht bewiesen
ist.
Es handelt sich um folgendes:
Nehmen Sie etwa den Körper R(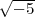 ). Die Normen x2 + 5y2 der ungeraden
Zahlen sind
). Die Normen x2 + 5y2 der ungeraden
Zahlen sind  1 (mod 4). Das Nichthauptideal
1 (mod 4). Das Nichthauptideal  = (3,1 +
= (3,1 + 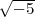 ) hat die
Norm 3
) hat die
Norm 3  -1 (mod 4), also sind die Normen aller ungeraden Ideale der
Nichthauptklasse
-1 (mod 4), also sind die Normen aller ungeraden Ideale der
Nichthauptklasse  -1 (mod 4). Erst recht findet man also in dieser Klasse kein
Ideal mit einer Norm
-1 (mod 4). Erst recht findet man also in dieser Klasse kein
Ideal mit einer Norm  1 (mod 12).
1 (mod 12).
Folglich versagt der Schäfersche Beweis und ebenso Ihr Beweis in diesem
Fall.
Ich habe versucht die Lücke auszufüllen, es ist mir aber nicht gelungen. Nur
Folgendes habe ich zu Stande gebracht:
Bewiesen ist: Ist N
 1 (mod 12), so gilt der Satz. Da nun das Quadrat
jedes zu 12 primen Ideals die Bedingung erfüllt, ist jedenfalls das Quadrat jedes
Ideals Hauptideal.
1 (mod 12), so gilt der Satz. Da nun das Quadrat
jedes zu 12 primen Ideals die Bedingung erfüllt, ist jedenfalls das Quadrat jedes
Ideals Hauptideal.
Führt man den Beweis für 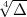 statt für
statt für 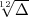 , so findet man: Ist N
, so findet man: Ist N
 1
(mod 4), so ist die dritte Potenz von
1
(mod 4), so ist die dritte Potenz von  Hauptideal also wegen des vorigen auch
Hauptideal also wegen des vorigen auch  selbst. Es gilt also schärfer:
selbst. Es gilt also schärfer:
Aus N
 1 (mod 4) folgt dass
1 (mod 4) folgt dass  Hauptideal. Der Hauptidealsatz ist also
nicht bewiesen für solche imaginär-quadratische k über denen k(i) unverzweigt
ist, denn dann gibt es nur eine Idealgruppe vom Index 2 mit N
Hauptideal. Der Hauptidealsatz ist also
nicht bewiesen für solche imaginär-quadratische k über denen k(i) unverzweigt
ist, denn dann gibt es nur eine Idealgruppe vom Index 2 mit N
 1 (mod 4)
und dem Führer 1. Das sind die Körper R(
1 (mod 4)
und dem Führer 1. Das sind die Körper R(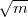 ) mit m≠ - 1 und m
) mit m≠ - 1 und m  3
(mod 4).
3
(mod 4).
Ein ganz kleines Stück kommt man noch weiter. Es genügt ein einziges Ideal  anzugeben, das Hauptideal wird und für das N
anzugeben, das Hauptideal wird und für das N
 -1 (mod 4) ist. Ist nun
p > 0 ein Primteiler von m der
-1 (mod 4) ist. Ist nun
p > 0 ein Primteiler von m der  -1 (mod 4) ist, p =
-1 (mod 4) ist, p =  2 in k, so ist
2 in k, so ist  ein solches Ideal. Es wird nämlich in k(
ein solches Ideal. Es wird nämlich in k(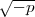 ) ersichtlich das Hauptideal
(
) ersichtlich das Hauptideal
(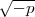 ) und dieser Körper ist im Klassenkörper enthalten. Es bleiben noch
diejenigen m, bei denen alle Primteiler
) und dieser Körper ist im Klassenkörper enthalten. Es bleiben noch
diejenigen m, bei denen alle Primteiler  1 (mod 4) sind (z.B. m = -5).
Das Ideal
1 (mod 4) sind (z.B. m = -5).
Das Ideal  = (2,1 +
= (2,1 + 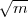 ) ist in k(i) das Hauptideal (1 + i). Bildet man
) ist in k(i) das Hauptideal (1 + i). Bildet man
 =
= 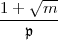 , so ist N
, so ist N =
= 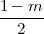 . Ist also m
. Ist also m  3 (mod 8), so ist
3 (mod 8), so ist  ein solches
Ideal.
ein solches
Ideal.
Es sind also unerledigt die Körper R(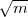 ) mit m
) mit m  -1 (mod 8) (etwa
R(
-1 (mod 8) (etwa
R(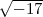 )), bei denen alle Primteiler von m die Form 4n + 1 haben.
)), bei denen alle Primteiler von m die Form 4n + 1 haben.
Weiter bin ich nicht gekommen und ich sehe auch keinen Weg dazu.
Darf ich bei dieser Gelegenheit noch auf eine kleine Unrichtigkeit
in Ihrer Arbeit hinweisen, die sich aber in Ordnung bringen lässt. Die
Transfomationsklasse 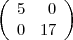 lässt sich nicht so normieren wie auf Seite 316
unten angegeben ist. Erreichen kann man nur
lässt sich nicht so normieren wie auf Seite 316
unten angegeben ist. Erreichen kann man nur
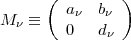 mit
b
mit
b
 0 (mod 12), a
0 (mod 12), a
 d
d (mod 12) und a
(mod 12) und a
 d
d
 1 (mod 4).
1 (mod 4).
Aber damit kommt man glücklicher Weise beim Beweis aus. Allerdings genügt
es nicht von  12(S) zu wissen, dass für S
12(S) zu wissen, dass für S  E (mod 12)
E (mod 12)  12(S) = 1 ist
(Seite 120), sondern es muss für S
12(S) = 1 ist
(Seite 120), sondern es muss für S 
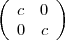 (mod 12) mit c
(mod 12) mit c  1
(mod 4)
1
(mod 4)  12(S) = 1 gezeigt werden. Das folgt etwa aus der Formel.
12(S) = 1 gezeigt werden. Das folgt etwa aus der Formel.
Vielleicht fällt Ihnen ein, wie man den Beweis zu Ende führen kann.
Wir haben uns sehr über Ihren Aufenthalt bei uns
gefreut .
Meine Frau liest andauernd in dem Buch.
Mit vielen Grüssen Ihr
Artin
Beste Grüße
N.
Artin
Kommentare zum Brief Nr.47:
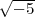 ). Die Normen x2 + 5y2 der ungeraden
Zahlen sind
). Die Normen x2 + 5y2 der ungeraden
Zahlen sind  1 (mod 4). Das Nichthauptideal
1 (mod 4). Das Nichthauptideal  = (3,1 +
= (3,1 + 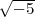 ) hat die
Norm 3
) hat die
Norm 3  -1 (mod 4), also sind die Normen aller ungeraden Ideale der
Nichthauptklasse
-1 (mod 4), also sind die Normen aller ungeraden Ideale der
Nichthauptklasse  -1 (mod 4). Erst recht findet man also in dieser Klasse kein
Ideal mit einer Norm
-1 (mod 4). Erst recht findet man also in dieser Klasse kein
Ideal mit einer Norm  1 (mod 12).
1 (mod 12).

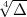 statt für
statt für 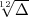 , so findet man: Ist
, so findet man: Ist 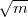
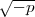
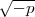
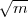
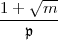 , so ist
, so ist 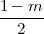
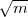
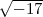
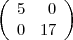 lässt sich nicht so normieren wie auf Seite 316
unten angegeben ist. Erreichen kann man nur
lässt sich nicht so normieren wie auf Seite 316
unten angegeben ist. Erreichen kann man nur