
Lieber Herr Hasse! 161
Noch einige Kleinigkeiten zum gestrigen Brief. Bezeichnungen wie gestern:

 = b
= b nc1-
nc1- a
a , so liefert a'
, so liefert a' „dasselbe“ Faktorensystem wie a
„dasselbe“ Faktorensystem wie a . Ich schreibe
dann a'
. Ich schreibe
dann a' ~ a
~ a auch dann wenn die a
auch dann wenn die a überhaupt kein Faktorensystem liefern, d.h.
sich keine n-te Idealpotenz ergibt.
überhaupt kein Faktorensystem liefern, d.h.
sich keine n-te Idealpotenz ergibt.
Liefern die a ein Faktorensystem, so folgt aus (2): Bei festem
ein Faktorensystem, so folgt aus (2): Bei festem  ist
a
ist
a
 ~ a
~ a a
a
 ; ebenso bei festem
; ebenso bei festem  und variablem
und variablem  .
.
Behauptet wird nicht, dass die a
 ein Faktorsystem ergeben. Nun folgt bei
festem
ein Faktorsystem ergeben. Nun folgt bei
festem  aus
aus 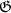 :
:
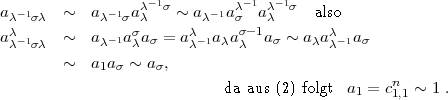
 -1
-1

 bei festem
bei festem  ein zu c
ein zu c ,
, äquivalentes Faktorensystem
äquivalentes Faktorensystem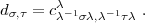
Dass bei beliebigem c ,
, auch d
auch d ,
, ein Faktorensystem ist, folgt unmittelbar
aus (3). Aber nur für Ideale ergibt sich seine Äquivalenz mit c
ein Faktorensystem ist, folgt unmittelbar
aus (3). Aber nur für Ideale ergibt sich seine Äquivalenz mit c ,
, . Es ist dies zu
bezeichnen als das durch Anwendung von
. Es ist dies zu
bezeichnen als das durch Anwendung von  aus c
aus c ,
, entstehende Faktorensystem.
Seine unsymmetrische Bauart rührt daher, dass in der Definition (4) eine Seite
ausgezeichnet ist. Daher darf nicht ohne weiteres c
entstehende Faktorensystem.
Seine unsymmetrische Bauart rührt daher, dass in der Definition (4) eine Seite
ausgezeichnet ist. Daher darf nicht ohne weiteres c ,
,
 genommen werden. Wir
haben also:
genommen werden. Wir
haben also:
Jedes ideale Faktorensystem ist invariant gegenüber der Gruppe 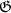 .
.
Nun zur gestrigen Berechnung der  -primären Faktorensysteme. Wenn Sie
eine Abbildung h
-primären Faktorensysteme. Wenn Sie
eine Abbildung h der Zerlegungsgruppe hernehmen, so gehört dazu ein
der Zerlegungsgruppe hernehmen, so gehört dazu ein
 -primäres Faktorsystem a
-primäres Faktorsystem a (
(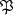 ). Ersetzen Sie
). Ersetzen Sie 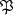 durch
durch 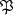
 , und in der
gruppentheoretischen Rechnung überall die Isomorphie
, und in der
gruppentheoretischen Rechnung überall die Isomorphie 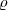


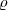
 -1, ferner sei
statt h
-1, ferner sei
statt h genommen h
genommen h -1
-1
 ,
,  aus
aus 

 -1, als Abbildung, so rechnen Sie leicht
nach, dass in diesem Sinn
-1, als Abbildung, so rechnen Sie leicht
nach, dass in diesem Sinn


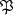 bei gegebener Abbildung „dasselbe“ Faktorsystem wie
bei gegebener Abbildung „dasselbe“ Faktorsystem wie 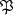 .
Ebenso leicht ist zu sehen, dass a
.
Ebenso leicht ist zu sehen, dass a (
(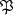 ) nicht davon abhängt (im Sinn der
Äquivalenz) welches Vertretersystem
) nicht davon abhängt (im Sinn der
Äquivalenz) welches Vertretersystem 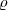 mod
mod  gewählt wird.
gewählt wird.
Es sei nun  kein Diskr[iminanten]teiler . Dann kann eine ausgezeichnete
Abbildung h
kein Diskr[iminanten]teiler . Dann kann eine ausgezeichnete
Abbildung h der Zerlegungsgruppe auf die Restklassen modulo n gegeben
werden. Nämlich h
der Zerlegungsgruppe auf die Restklassen modulo n gegeben
werden. Nämlich h![[K-]
P](hasart-web-080922762x.png)

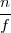 (mod n), wo
(mod n), wo ![[ ]
K-
P](hasart-web-080922764x.png) das Frobenius’sche Symbol ist.
Dann ist also jedem Primideal
das Frobenius’sche Symbol ist.
Dann ist also jedem Primideal  ein ganz bestimmtes Faktorsystem cik(
ein ganz bestimmtes Faktorsystem cik( )
zugeordnet.
)
zugeordnet.
Frage: Darf man es wagen, das Reziprozitätsgesetz im Anschluss an das gestrige Zerlegungsgesetz zu formulieren? Wie ist klar.
Mit besten Grüssen
Ihr Artin
Die Invarianz bei  der c
der c ,
, kann auch für Zahlen aber auf anderem Wege
gezeigt werden. Innerer Automorphismus mit u
kann auch für Zahlen aber auf anderem Wege
gezeigt werden. Innerer Automorphismus mit u der Algebra.
der Algebra.