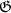 Gruppe, c
Gruppe, c ,
, Faktorsystem zu u
Faktorsystem zu u mit Relationen
mit Relationen
Lieber Herr Hasse!
Vielen Dank für den Sonderabdruck und Ihren Brief. Ich habe inzwischen auch über die Dinge nachgedacht, formuliere sie aber noch anders. Ich möchte Ihnen darüber berichten bemerke aber dass Sie die Formeln noch in Ihre Schreibweise umschreiben müssen, da ich die Reihenfolge verkehrt nehme, mich aber daran gewöhnt habe.
1.) K Körper, 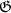 Gruppe, c
Gruppe, c ,
, Faktorsystem zu u
Faktorsystem zu u mit Relationen
mit Relationen
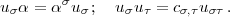
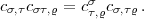
 zu v
zu v =
= 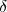
 u
u führt auf das Faktorsystem
führt auf das Faktorsystem
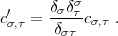
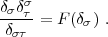
2.) Setzen Sie 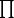
 c
c ,
, = a
= a ;
; 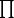
 c
c ,
, = b
= b , so ergibt die Assoziativitätsrelation,
wenn man die Produkte über
, so ergibt die Assoziativitätsrelation,
wenn man die Produkte über  oder über
oder über  oder über
oder über 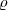 durch die ganze Gruppe
bildet, die drei folgenden Relationen (N = Norm K/k):
durch die ganze Gruppe
bildet, die drei folgenden Relationen (N = Norm K/k):
b b b = N(c = N(c , , )b )b  | oder N(c , , ) = ) = 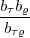 | (1) |
a b b = b = b  a a
 | oder b  -1 = 1, also ist b -1 = 1, also ist b
 ambig. ambig. | (2) |
c , , na na
  = a = a  a a
 | oder c , , n = n = 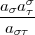 | (3) |
Die dritte Relation ist die wichtigste. Sie zeigt wohl am schnellsten und leichtesten sowohl für Zahlen wie für Ideale den Satz, dass die n-te Potenz jedes Faktorensystems ~ (1) ist.
3.) F(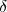
 ) = 1
) = 1 
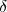
 = a1-
= a1- wo a =
wo a = 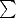

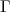

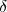
 ≠0 .
≠0 .
Sowohl für Zahlen wie für Ideale.156
4.) Unter dem  -Beitrag eines idealen F[aktor]s[ystems] verstehe ich
den Beitrag, den die Teiler von
-Beitrag eines idealen F[aktor]s[ystems] verstehe ich
den Beitrag, den die Teiler von  zu c
zu c ,
, liefern. Ein Faktorsystem
das nur aus
liefern. Ein Faktorsystem
das nur aus  -Teilern besteht nenne ich ein primäres. Dann ist jedes
Faktorsystem eindeutig Produkt von zu verschiedenen
-Teilern besteht nenne ich ein primäres. Dann ist jedes
Faktorsystem eindeutig Produkt von zu verschiedenen  gehörigen
primären.157
gehörigen
primären.157
5.) Ich bestimme die Gruppe aller  -primären Faktorensysteme modulo den ~
(1):
-primären Faktorensysteme modulo den ~
(1):
Wegen (3) ist c ,
, n =
n = 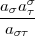 für jedes Faktorsystem c
für jedes Faktorsystem c ,
, . Ist darin a
. Ist darin a beliebiges
Ideal aber so, dass eine n-te Idealpotenz herauskommt, so ist das so bestimmte
c
beliebiges
Ideal aber so, dass eine n-te Idealpotenz herauskommt, so ist das so bestimmte
c ,
, ein ideales Faktorsystem. Man setze:
ein ideales Faktorsystem. Man setze:
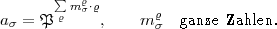
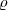 durchlaufe ein Vertretersystem von
durchlaufe ein Vertretersystem von 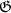 mod
mod 
 , also
, also
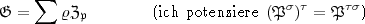

 von
von 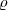 nur gemäss der Restkl[asse] abhängen
soll. Ist also z beliebiges Element von
nur gemäss der Restkl[asse] abhängen
soll. Ist also z beliebiges Element von 
 = Zerlegungsgruppe, so soll
gelten
= Zerlegungsgruppe, so soll
gelten
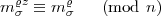 | (4) |
Damit eine n-te Potenz herauskommt muss gelten:
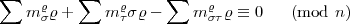 |
Dabei sind die 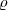 nur mod
nur mod 
 zu verstehen. Ersetzt man im mittleren Glied
zu verstehen. Ersetzt man im mittleren Glied 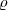 durch
durch  -1
-1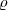 , so erhält man:
, so erhält man:
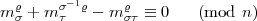 | (5) |
und man hat die Kongruenzen (4), (5) aufzulösen.
Man setze in (5) 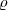 = 1 und
erhält158 ,
wenn man kurz m
= 1 und
erhält158 ,
wenn man kurz m statt m
statt m 1 schreibt:
1 schreibt:
m  -1 -1
|  m m  - m - m (mod n) also (mod n) also | ||
m  |  m m
 -1 -1 - m - m -1 (mod n). -1 (mod n). | (6) |
 -1
-1 und
und  -1 beliebige
Paare sind, so folgt:
-1 beliebige
Paare sind, so folgt:
mz - mz - mz |  m m - m - m (mod n) (mod n) | (7) |
für jedes z    . Wenn . Wenn | ||
h | = m - m1 - m1 | (8) |
| gesetzt wird, so folgt | ||
hz - hz - hz |  h h - h - h . . | (7' ) |
 = 1, so folgt
= 1, so folgt
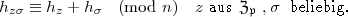 | (9) |
Aus (9) folgt (7') wieder identisch. Aus (8) folgt
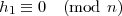 | (10) |
Jetzt ist im Ganzen:
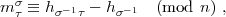 | (11) |
wobei (4) und 5 gelten wenn 9 gilt.
(9) kann, wenn die Werte hz bekannt sind, als Definition der Werte für die
Restklasse 
 gelten wenn h
gelten wenn h bekannt ist. Dann braucht also (9) nur noch für den
Spezialfall
bekannt ist. Dann braucht also (9) nur noch für den
Spezialfall 


 zu gelten. Also muss hz eine isomorphe Abbildung von
zu gelten. Also muss hz eine isomorphe Abbildung von  auf159
die additive Gruppe der Restklassen mod n bedeuten. Das ist alles was
bleibt.
auf159
die additive Gruppe der Restklassen mod n bedeuten. Das ist alles was
bleibt.
Setzen wir jetzt (11) ein in a so kommt, wenn wir n-te Potenzen zu einer
n-ten Idealpotenz b
so kommt, wenn wir n-te Potenzen zu einer
n-ten Idealpotenz b n vereinigen: (Wir rechnen ja modn.)
n vereinigen: (Wir rechnen ja modn.)
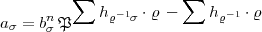
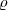 im Index ein ganz bestimmtes Vertretersystem durchläuft, sonst aber nur
mod
im Index ein ganz bestimmtes Vertretersystem durchläuft, sonst aber nur
mod  zu gehen braucht. Wir addieren im Exponenten die Summe
zu gehen braucht. Wir addieren im Exponenten die Summe
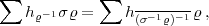
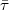 der ausgezeichnete Vertreter der Klasse von
der ausgezeichnete Vertreter der Klasse von  ist:
ist:
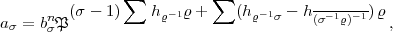
 -1
-1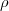 = (
= ( -1
-1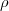 ) . z-1 mit einem bestimmten z aus
) . z-1 mit einem bestimmten z aus  , also ist
, also ist
(12)  = b
= b nc1-
nc1- .
.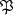
 hz .
hz . 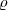
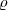 -1
-1 (
( -1
-1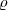 )
)
Geht man die z, die auftreten können durch, so kommt nach Reidemeister (es
sind seine Erzeugenden) sicher Erzeugende von  darunter vor. Ist also hz nicht
die identische Darstellung in den Restklassen, so ist der Exponent nicht immer
darunter vor. Ist also hz nicht
die identische Darstellung in den Restklassen, so ist der Exponent nicht immer
 0 (mod n). Ein a
0 (mod n). Ein a der Form b
der Form b nc1-
nc1- mit beliebigem b
mit beliebigem b und c liefert aber, wie
Sie sofort sehen, lauter hz
und c liefert aber, wie
Sie sofort sehen, lauter hz  0 (mod n).
0 (mod n).
Also ist a modulo b
modulo b nc1-
nc1- genau durch die Darstellung hz von
genau durch die Darstellung hz von  in den
Restklassen mod n gegeben, und dem Produkt von zwei a
in den
Restklassen mod n gegeben, und dem Produkt von zwei a -Vektoren ist die
Summe der hz zugeordnet.
-Vektoren ist die
Summe der hz zugeordnet.
Ein a der Form b
der Form b nc1-
nc1- liefert nun gemäss (3) ein c
liefert nun gemäss (3) ein c ,
, =
= 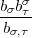 ~ 1. Also ist
die Gruppe der
~ 1. Also ist
die Gruppe der  -primären c
-primären c ,
, mod den ~ 1 isomorph mit der Gruppe aller
Darstellungen von
mod den ~ 1 isomorph mit der Gruppe aller
Darstellungen von 
 durch Restklassen modulo n. Diese Gruppe aber ist
isomorph mit der Faktorkommutatorgruppe von
durch Restklassen modulo n. Diese Gruppe aber ist
isomorph mit der Faktorkommutatorgruppe von 
 . Also:
. Also:
Die gesuchte Gruppe der  -primären c
-primären c ,
, ist isomorph mit der
Faktorkommutatorgruppe von
ist isomorph mit der
Faktorkommutatorgruppe von 
 .
.
Ist insbesondere  kein Diskriminantenteiler, so ist die Gruppe cyklisch von
der Ordnung f. Dann ist also f die kleinste Zahl so dass die f-te Potenz jedes
kein Diskriminantenteiler, so ist die Gruppe cyklisch von
der Ordnung f. Dann ist also f die kleinste Zahl so dass die f-te Potenz jedes
 -primären Faktorsystems ~ 1 ist.
-primären Faktorsystems ~ 1 ist.
Nun ist es wohl klar wie das Zerlegungsgesetz lautet:
Es sei 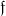 ein passender Modul.
ein passender Modul.  zerfällt dann und nur dann in Primideale
f-ten Grades, wenn f die Ordnung der
zerfällt dann und nur dann in Primideale
f-ten Grades, wenn f die Ordnung der  -primären Faktorensysteme modulo der
Gruppe
-primären Faktorensysteme modulo der
Gruppe
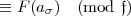
 zerfällt vollständig, wenn jedes
zerfällt vollständig, wenn jedes  -primäre Faktorsystem
-primäre Faktorsystem  F(a
F(a ) (mod
) (mod 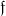 )
ist.
)
ist.
Ich habe noch keine Zeit gehabt über den Beweis nachzudenken der nicht schwer sein kann. Ich habe nur den abelschen Spezialfall Gruppe (2,2) und die symmetrische Gruppe der Ordnung 6 geprüft also den Fall des kubischen Körpers. Es ist alles in Ordnung und stimmt in diesen Fällen. Im abelschen Fall lässt sich alles im Grundkörper normieren und führt auf die alte K[lassen]körpert[heorie.]
Im nicht abelschen Fall kommt einfach die alte Methode heraus die Klassenkörpertheorie anzuwenden auf Unterkörper in bezug auf die der ganze Körper cyklisch ist. So muss auch der Beweis mühelos herauskommen. Es ergibt sich also nur das eine Neue am Zerlegungsgesetz, dass es invariant formuliert und die verschiedenen Gruppen in den verschiedenen Körpern in einheitlichen und übersichtlichen Zusammenhang gebracht sind.
Dagegen kann natürlich keine Rede von einer Isomorphie sein. Im
symm[etrischen] Fall 6 kommen für die Faktorensysteme modulo F(a ) (mod
) (mod 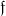 ) 6
Klassen heraus (natürlich cyklisch):
) 6
Klassen heraus (natürlich cyklisch):
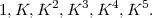
 ,
, , wie aus
dem Zerl[egungs]ges[etz] folgt, da es keine unzerlegt bleibenden
, wie aus
dem Zerl[egungs]ges[etz] folgt, da es keine unzerlegt bleibenden  gibt. Wohl aber
gibt es in K und K5 Faktorensysteme. Etwa das Produkt eines primären der
Ordnung 2 mit einem der Ordnung 3. In diesem Fall ist wie gesagt alles
bewiesen.
gibt. Wohl aber
gibt es in K und K5 Faktorensysteme. Etwa das Produkt eines primären der
Ordnung 2 mit einem der Ordnung 3. In diesem Fall ist wie gesagt alles
bewiesen.
Bei einer endgültigen Darstellung werden natürlich die Rechnungen dann zu vermeiden sein, wenn auf die abstrakte Bedeutung des verschränkten Produkts mit Idealen eingegangen wird. Die Bedeutung ist diese:
Sei 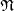 die Gruppe aller Ideale,
die Gruppe aller Ideale, 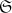 die Gruppe aller au
die Gruppe aller au . Dann ist
. Dann ist 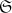 gekennzeichnet als Erweiterung von
gekennzeichnet als Erweiterung von 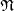 die
die
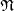 als Normalteiler enhält,
als Normalteiler enhält,
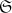 /
/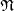

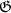 ,
,
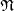 die Isomorphismen von
die Isomorphismen von 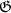 .
.Die Komposition der Faktorensysteme lässt sich zwar invariant in naheliegender Weise deuten, aber nicht schön.
Selbst werden Sie sich wohl überlegt haben, wie die Faktorensysteme abzuändern sind wenn man Erzeugende und Relationen einführt. Das übliche Faktorsystem ist nur der Fall der Cayleyschen Gruppentafel.
Ich habe den Eindruck, dass noch etwas ganz Neues hinzukommen muss um zu Isomorphie und zu Existenzsätzen zu kommen. Dieses Zerlegungsgesetz ist nur eine etwas verschönte Zusammenfassung der Anwendung der gewöhnlichen Klassenkörpertheorie .
Mit vielen herzlichen Grüssen von Haus zu Haus
Ihr Artin
Kommentare zum Brief Nr. 42: