42.1 Der erste Brief über Faktorensysteme.
Dieser Brief ist der Beginn einer Serie von 5 Briefen, in denen Artin die
Grundregeln des Rechnens mit Faktorensystemen entwickelt. Faktorensysteme waren
aufgetaucht in der Theorie der Algebren, oder „hyperkomplexen Systeme“ wie
Emmy Noether sie nannte. In ihrer Göttinger Vorlesung 1929 hatte Noether diese
Faktorensysteme eingeführt und gezeigt, dass sich jede einfache zentrale Algebra
A als verschränktes Produkt mit einem geeigneten Faktorensystem darstellen
läßt.
Ist k der Grundkörper und K|k ein galoisscher Zerfällungskörper mit
Galoisgruppe 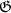 , so ist A eindeutig (bis auf Äquivalenz) charakterisiert durch das
zugehörige Element in der Kohomologiegruppe H2(
, so ist A eindeutig (bis auf Äquivalenz) charakterisiert durch das
zugehörige Element in der Kohomologiegruppe H2(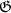 ,K×). Zur damaligen Zeit
gab es jedoch noch keine algebraische Kohomologietheorie, und daher rechnete
man explizit mit Faktorensystemen modulo zerfallenden Faktorensystemen.
Emmy Noether hat ihre Theorie der Faktorensysteme niemals publiziert. Sie
hatte jedoch Hasse die Erlaubnis gegeben, diese Theorie in seiner amerikanischen
Arbeit über zyklische Algebren darzustellen. Diese Arbeit ist 1932 in den
Transactions of the American Mathematical Society erschienen [Has32b]. Später
ging die Theorie der Faktorensysteme in den Ergebnisbericht von Deuring über
Algebren ein [Deu35a].
,K×). Zur damaligen Zeit
gab es jedoch noch keine algebraische Kohomologietheorie, und daher rechnete
man explizit mit Faktorensystemen modulo zerfallenden Faktorensystemen.
Emmy Noether hat ihre Theorie der Faktorensysteme niemals publiziert. Sie
hatte jedoch Hasse die Erlaubnis gegeben, diese Theorie in seiner amerikanischen
Arbeit über zyklische Algebren darzustellen. Diese Arbeit ist 1932 in den
Transactions of the American Mathematical Society erschienen [Has32b]. Später
ging die Theorie der Faktorensysteme in den Ergebnisbericht von Deuring über
Algebren ein [Deu35a].
Wir können annehmen, dass Artin über die Noethersche Theorie informiert
war.
Seit seiner Studienzeit war es für Artin ein zentrales Problem, an das
Zerlegungsgesetz für nicht-abelsche galoissche Erweiterungen zu gelangen. Damals
hegte man die Hoffnung, dass die Faktorensysteme einen Zugang zu dieser
Frage öffnen können. Das war sicherlich eine Motivation Artins bei seinen
Rechnungen mit Faktorensystemen. Wenn sich Artin in seinem Brief bei Hasse
für „den Sonderabdruck“ bedankt, dann handelt es sich wahrscheinlich
um den Sonderabdruck der Arbeit von Brauer-Hasse-Noether über das
Lokal-Global-Prinzip für Algebren; die Arbeit war in dem Hensel-Festband des
Crelleschen Journals Anfang Januar 1931 erschienen. Am Schluss dieser Arbeit
werden Folgerungen für galoissche, nicht notwendig abelsche Erweiterungen von
Zahlkörpern diskutiert, und es heißt:
„Man kommt so zu Sätzen, die als
Verallgemeinerung von Hauptsätzen der Klassenkörpertheorie…
auf allgemeine relativ-galoissche Zahlkörper anzusehen sind.“
Wahrscheinlich hatte Hasse in seinem Brief an Artin hierauf hingewiesen und
auch noch ein paar weitergehende Überlegungen mitgeteilt. So ist es zu
verstehen, wenn Artin sagt, er habe „inzwischen auch über die Dinge
nachgedacht“.
Der von Hasse in der genannten Crelle-Arbeit aufgestellte Zerlegungssatz für
eine galoissche Zahlkörpererweiterung K|k mit Gruppe 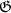 bezieht sich auf die
Brauer-Gruppe Br(K|k) der von K zerfällten einfachen zentralen k-Algebren. Es
sei
bezieht sich auf die
Brauer-Gruppe Br(K|k) der von K zerfällten einfachen zentralen k-Algebren. Es
sei  ein Primideal aus k, das in K nicht verzweigt ist, und f der Relativgrad der
Primteiler von
ein Primideal aus k, das in K nicht verzweigt ist, und f der Relativgrad der
Primteiler von  in K. Dann gilt:
in K. Dann gilt:
Zerlegungssatz: f ist der kleinste Exponent, für den A f ~ 1
für alle Algebren A
f ~ 1
für alle Algebren A  Br(K|k).
Br(K|k).
Allerdings entspricht dieser Satz nicht recht den Erwartungen, die
man an die Klassenkörpertheorie galoisscher Erweiterungen stellte. Die
Brauergruppe Br(K|k) ist eine unendliche Gruppe (falls nicht der triviale Fall
K = k vorliegt), und man kann daher Br(K|k) nicht als äquivalent für die
Strahlklassengruppen aus der abelschen Klassenkörpertheorie ansehen. Man
suchte daher, ausgehend von dem obigen Zerlegungssatz, nach anderen
Beschreibungen der Zerlegung von Primidealen  , d.h. nach einer Beschreibung
des Relativgrades f von
, d.h. nach einer Beschreibung
des Relativgrades f von  . Das ist der Ausgangspunkt der Artinschen
Rechnungen.
. Das ist der Ausgangspunkt der Artinschen
Rechnungen.
Diese Rechnungen zeichnen sich aus durch ihren abstrakten Ansatz. Artin
abstrahiert von der Deutung der Faktorensysteme als Bestimmungsstücke für
Algebren, und er benutzt lediglich die formalen Rechenregeln.Das kommt
besonders deutlich zum Ausdruck in dem Beweis der Formel (3) in Abschnitt 2.),
welche besagt, dass die Gruppenordnung die 2-Kohomologie annulliert. Diese
Rechnung ist nichts anderes als eine Übung im Rechnen mit 2-Kohomologie in
einem (multiplikativ geschriebenen) 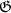 -Modul. Und mehrere andere Passagen
haben denselben Charakter, so z.Bsp. in Abschnitt 5.), wo das heute so
genannte „Lemma von Shapiro“ für die 2-Kohomologie bewiesen wird; dadurch
wird die Berechnung der
-Modul. Und mehrere andere Passagen
haben denselben Charakter, so z.Bsp. in Abschnitt 5.), wo das heute so
genannte „Lemma von Shapiro“ für die 2-Kohomologie bewiesen wird; dadurch
wird die Berechnung der  -adischen 2-Kohomologie zurückgeführt auf die
Zerlegungsgruppe
-adischen 2-Kohomologie zurückgeführt auf die
Zerlegungsgruppe 
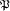 zu einem Primidealteiler
zu einem Primidealteiler 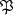 von
von  , auf dessen Wahl es nicht
ankommt.
, auf dessen Wahl es nicht
ankommt.
Heute würden wir die Artinschen Rechnungen wie folgt beschreiben: Es
bedeute D die Gruppe derjenigen Ideale von K, die nur Primteiler
die Gruppe derjenigen Ideale von K, die nur Primteiler 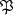 von
von  enthalten. Es ist dann D
enthalten. Es ist dann D die direkte Summe
die direkte Summe
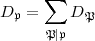
wobei D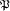 die von
die von 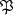 erzeugte zyklische Gruppe bedeutet; sie ist zu
erzeugte zyklische Gruppe bedeutet; sie ist zu 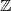 isomorph.
Nach dem „Lemma von Shapiro“ ist dann
isomorph.
Nach dem „Lemma von Shapiro“ ist dann
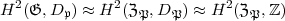
wobei der zweite und dritte Term sich auf ein festgewähltes 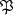 |
| beziehen. Artin
schreibt für die Zerlegungsgruppe
beziehen. Artin
schreibt für die Zerlegungsgruppe 
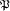 auch einfach
auch einfach  . Sei n die Ordnung von
. Sei n die Ordnung von 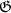 .
Aus der exakten Sequenz
.
Aus der exakten Sequenz
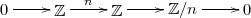
lesen wir ab, dass
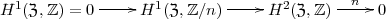
und somit
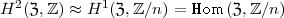
wobei rechts die Charaktergruppe von  steht, die isomorph ist zur
Faktorkommutatorgruppe von
steht, die isomorph ist zur
Faktorkommutatorgruppe von  . Die obige Rechnung gilt für alle
. Die obige Rechnung gilt für alle  , ob verzweigt
oder nicht. Wenn nun
, ob verzweigt
oder nicht. Wenn nun  unverzweigt ist, dann ist die Zerlegungsgruppe
unverzweigt ist, dann ist die Zerlegungsgruppe  zyklisch,
und dasselbe gilt dann für ihre Charaktergruppe.
zyklisch,
und dasselbe gilt dann für ihre Charaktergruppe.
All diese Isomorphismen werden von Artin explizit ausgerechnet. Er kann
somit einem Faktorensystem c ,
, von
von 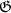 in K× für jedes Ideal
in K× für jedes Ideal  einen
Charakter h der Zerlegungsgruppe
einen
Charakter h der Zerlegungsgruppe 
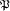 zuordnen. Im unverzweigten Fall ist der
Frobenius-Automorphismus definiert, den Artin als
zuordnen. Im unverzweigten Fall ist der
Frobenius-Automorphismus definiert, den Artin als ![[ ]
KP-](hasart-web-080922757x.png) bezeichnet. Die
Anwendung von h liefert dann eine bestimmte Restklasse modulo n, und nach
Division mit n eine bestimmte Restklasse modulo 1. Artin stellt fest (im Brief
Nr.45), dass dies genau die
bezeichnet. Die
Anwendung von h liefert dann eine bestimmte Restklasse modulo n, und nach
Division mit n eine bestimmte Restklasse modulo 1. Artin stellt fest (im Brief
Nr.45), dass dies genau die  -adische Hasse-Invariante der durch c
-adische Hasse-Invariante der durch c ,
, definierten
einfachen Algebra ist.
definierten
einfachen Algebra ist.
In Richtung einer nicht-abelschen Klassenkörpertheorie ist das Ergebnis der
Rechnungen jedoch für Artin enttäuschend. Er stellt fest, dass im nichtabelschen
Fall einfach die
„alte Methode herauskommt, die Klassenkörpertheorie
anzuwenden auf Unterkörper in Bezug auf die der ganze Körper
zyklisch ist“.
Und er sagt:
„Ich habe den Eindruck, dass noch etwas ganz Neues
hinzukommen muss…“
Die weitere Entwicklung hat dies bestätigt. Bemerkenswert ist, dass Artin
dies schon so früh erkannt hat, schon im März 1932. Allerdings hatte
man damals noch keine Vorstellung davon, wie diese ganz neuen Ideen
aussehen könnten. Die Klassenkörpertheorie für galoissche Erweiterungen
hat erst viel später durch die Ideen von Langlands einen neuen Impetus
erfahren.
Die Artinschen Versuche in diesen Briefen, ein „Zerlegungsgesetz“ als
Kongruenzbedingung für die Faktorensysteme nach einem geeigneten Modul zu
formulieren, sind also im nichtabelschen Fall nicht gelungen. Immerhin sind die
Artinschen Rechnungen als ein erster Schritt anzusehen, die gesamte
Klassenkörpertheorie auf der Kohomologietheorie aufzubauen. Nachdem der
Formalismus der Kohomologie der Gruppen hinreichend weit entwickelt worden
war, stellte sich heraus, dass dies ein sehr starkes Hilfsmittel zur Behandlung der
Klassenkörpertheorie wurde. Sie gipfelte schließlich in dem bekannten Werk von
Artin-Tate [AT68].
Wir können feststellen, dass diese Entwicklung mit den hier vorliegenden
Artin-Briefen ihren Anfang genommen hat.
Hasse jedoch hat die Durchdringung der Klassenkörpertheorie mit Begriffen
und Methoden der Kohomologietheorie nicht mehr in demselben Maße
mitgetragen. In seinem Vortrag über die Geschichte der Klassenkörpertheorie
[Has66] äußert er seine Meinung, dass dadurch „die scharf profilierten Linien und
individuellen Züge“ der Klassenkörpertheorie „an Leuchtkraft und Plastizität
etwas eingebüßt haben.“ Damit meinte er, dass in den Algebren noch viel mehr
arithmetische Informationen enthalten seien, die nicht allein durch die
Kohomologie erfasst werden; so etwa hat er sich zu uns bei mehreren
Gelegenheiten geäußert.
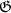 , so ist A eindeutig (bis auf Äquivalenz) charakterisiert durch das
zugehörige Element in der Kohomologiegruppe H2(
, so ist A eindeutig (bis auf Äquivalenz) charakterisiert durch das
zugehörige Element in der Kohomologiegruppe H2(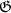 ,K×). Zur damaligen Zeit
gab es jedoch noch keine algebraische Kohomologietheorie, und daher rechnete
man explizit mit Faktorensystemen modulo zerfallenden Faktorensystemen.
Emmy Noether hat ihre Theorie der Faktorensysteme niemals publiziert. Sie
hatte jedoch Hasse die Erlaubnis gegeben, diese Theorie in seiner amerikanischen
Arbeit über zyklische Algebren darzustellen. Diese Arbeit ist 1932 in den
Transactions of the American Mathematical Society erschienen [Has32b]. Später
ging die Theorie der Faktorensysteme in den Ergebnisbericht von Deuring über
Algebren ein [Deu35a].
,K×). Zur damaligen Zeit
gab es jedoch noch keine algebraische Kohomologietheorie, und daher rechnete
man explizit mit Faktorensystemen modulo zerfallenden Faktorensystemen.
Emmy Noether hat ihre Theorie der Faktorensysteme niemals publiziert. Sie
hatte jedoch Hasse die Erlaubnis gegeben, diese Theorie in seiner amerikanischen
Arbeit über zyklische Algebren darzustellen. Diese Arbeit ist 1932 in den
Transactions of the American Mathematical Society erschienen [Has32b]. Später
ging die Theorie der Faktorensysteme in den Ergebnisbericht von Deuring über
Algebren ein [Deu35a].




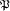
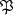
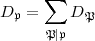
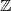
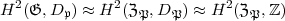
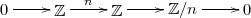
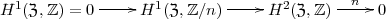
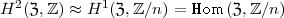
 ,
,
![[ ]
KP-](hasart-web-080922757x.png) bezeichnet. Die
Anwendung von
bezeichnet. Die
Anwendung von