11. März 1932162
Lieber Herr Hasse!
Aus meinen erneuten Rechnungen geht mit Deutlichkeit hervor, dass nur die primären idealen Faktorsysteme von Bedeutung sind. Die anderen sind relativ belanglos. 163
Heute habe ich den Fall eines abelschen Körpers behandelt. Ergebnis:
Jedes ideale Faktorsystem (primär oder nicht) lässt sich in ein symmetrisches ambiges transformieren:
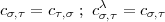
lassen sich so wählen, dass ohne Faktoren uu
= uu gilt.
Also ist das ganze Faktorsystem im Wesentlichen, d.h. bis auf die noch im
Oberkörper tatsächlich möglichen Transformationen die seine Form festlassen
gekennzeichnet durch ambige Ideale. Nimmt man Faktorensysteme, die prim zur
Diskr[iminante] sind, so handelt es sich um Ideale des Grundkörpers. Damit ist
die Frage geklärt, warum sich im abelschen Fall die Idealtheorie im Grundkörper
behandeln lässt, die Theorie der Zahlen dagegen nicht. Denn Zahlfaktorensysteme
lassen sich nicht in den Grundkörper transformieren.
Mit besten Grüssen
Ihr Artin
P.S. Die im gestrigen Nachsatz angedeutete Methode ist auch für Ideale besser und einfacher.