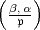15.3 Das Konzept zum Klassenkörperbericht II

Wir wissen nicht genau, woraus die „Sendung“ von Hasse bestanden hat, für die sich Artin bedankt. Aus dem Zusammenhang scheint hervorzugehen, dass Hasse ihm ein frühes Konzept für den Teil II seines Klassenkörperberichts [Has30a] geschickt hatte. Schließlich war das Konzept dieses Teils II vollständig auf das Artinsche Reziprozitätsgesetz als Grundlage ausgerichtet.

Wir entnehmen diesem und anderen Briefen Artins, dass er das Konzept und die Niederschrift des Hasseschen Klassenkörperberichts II in den verschiedenen Stadien interessiert beobachtet und kommentiert hat. Und Hasse hat ihn offenbar laufend informiert.

15.3.1 Der Zerlegungssatz

Der von Artin erwähnte „Zerlegungssatz“ findet sich in §11 des Klassenkörperberichts II. Und zwar bezieht sich dieser Satz auf das Hilbertsche Symbol 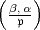für zwei Elemente , aus einem Zahlkörper k ¹²⁷ . Eigentlich handelt es sich um zwei Zerlegungssätze:

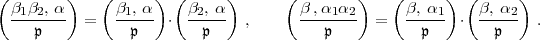Diese bedeuten, dass das Hilbertsche Symbol in jeder der beiden Variablen multiplikativ ist. Hasse nennt die erste Relation den „vorderen“ Zerlegungssatz, weil er sich auf die vordere Variable bezieht. Entsprechend wird die zweite Formel als „hinterer“ Zerlegungssatz bezeichnet. Natürlich sind diese beiden Zerlegungssätze gleichbedeutend zufolge der bekannten „Vertauschungsregel“

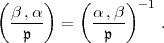In Hasses Aufbau im Klassenkörperbericht II wird jedoch bei dem Beweis der Vertauschungsregel sowohl der vordere als auch der hintere Zerlegungssatz benutzt, die demzufolge zuerst getrennt bewiesen werden.

Das Hilbertsche Symbol bezieht sich auf einen vorgegebenen Exponenten m, und es wird in diesem Zusammenhang stets vorausgesetzt, dass die m-ten Einheitswurzeln im Grundkörper k liegen. Hier setzt nun die Frage Artins ein: Kann der Beweis des Zerlegungssatzes nicht auch geführt werden, wenn die m-ten Einheitswurzeln nicht in k liegen? Auf den ersten Blick erscheint diese Frage sinnlos, weil ja das Hilbertsche Symbol garnicht definiert ist, wenn nicht die einschlägigen Einheitswurzeln im Grundkörper liegen. Die Frage erscheint jedoch verständlich, wenn man die Hassesche neue Definition des Hilbert-Symbols berücksichtigt.

Denn Hasse definiert das Hilbert-Symbol mit Hilfe des Normsymbols 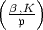, das von ihm im Anschluss an das Artinsche Reziprozitätsgesetz eingeführt wird. Dabei ist K eine beliebige abelsche Erweiterung von k, und k^×. Wir berichten darüber in 26.1.¹²⁸ Die Werte dieses Normsymbols liegen in der Galoisgruppe von K|k. Wenn Artin sich mit Hasses „Formalisierung“ einverstanden erklärt, so bezieht er sich darauf, dass Hasse die Definition dieses Normsymbols zunächst ganz formal ohne Bezug auf Normen gibt und auch die einschlägigen funktoriellen Eigenschaften auf diese formale Definition gründet; erst danach wird die Normeigenschaft gezeigt (das heißt: die durch 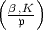gegebene Abbildung ist ein Isomorphismus der -lokalen Normgruppe auf die Zerlegungsgruppe von ).

In der Definition des Normsymbols 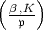wird nicht vorausgesetzt, dass die m-ten Einheitswurzeln im Grundkörper liegen. Artins Frage bezieht sich also wahrscheinlich auf diesen Fall und er meint, dass bei Hasse hier die zum „Zerlegungssatz“ analogen Formeln fehlen. Er fordert Hasse auf, diese Lücke zu schliessen. In der endgültigen Fassung des Klassenkörperberichts II, §6 finden sich diese Formeln, nämlich:

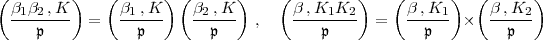wobei K₁K₂ ein Kompositum abelscher Körper über k bezeichnet.¹²⁹

Der „Zerlegungssatz“ für das Hilbertsche Symbol beruht nun in Hasses Klassenkörperbericht II direkt auf diesen Formeln für das Normsymbol . Und zwar ist das evident aufgrund der Hasseschen Definition des Hilbertschen Symbols (für gegebenen Exponenten m), die wie folgt lautet:

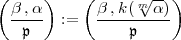(33)

Dabei ist vorauszusetzen, dass in k(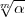) unverzweigt ist, d.h. dass m-primär ist für .

Wir halten es für unwahrscheinlich, dass Hasse dies nicht auch in seiner Sendung an Artin erwähnt hat. Wir nehmen daher an, dass Artin hier „etwas übersehen“ hat, was er ja auch selbst in seinem Brief als möglich andeutet. Es ist aber auch denkbar, dass Hasse in seinem frühen Konzept einen anderen Beweis des Zerlegungssatzes für das Hilbertsche Symbol im Auge hatte, vielleicht in Verallgemeinerung seiner früheren Arbeit [Has25c] aus dem Jahre 1925 im Falle m = . Wir kennen jedoch jenes frühe Konzept nicht, falls es überhaupt existiert hat.

15.3.2 Das Eisensteinsche Reziprozitätsgesetz

Artin fragt an, ob sich jetzt das Eisensteinsche Reziprozitätsgesetz „rasch“ beweisen läßt. Wir wissen nicht, was Hasse darauf geantwortet hat. In §16 des Klassenkörperberichts II leitet Hasse das Eisensteinsche Reziprozitätsgesetz für den Fall einer ungeraden Primzahl m = her, über dem -ten Einheitswurzelkörper k = (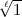). Aber die dortige Herleitung kann man wohl nicht als „rasch“ bezeichnen. Sie beruht auf der Produktformel für das Hilbertsche Symbol, und die daran anschließenden Rechnungen sind dann dem Typus nach dieselben, die auch schon vorher, ohne das Artinsche Reziprozitätsgesetz, durchgeführt wurden.

Hasses „Ansätze zu ⁿ-primär“, die Artin in seinem Brief erwähnt, sind wahrscheinlich in §14 des Klassenkörperberichts II eingegangen. Als „vernünftige“ Definition von 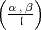, die Artin anmahnt¹³⁰ , ist wahrscheinlich noch nicht die Definition in §11 des Hasseschen Klassenkörperberichts II anzusehen. Denn in der dortigen, der obigen Formel (33) entsprechenden Definition mit Hilfe des Normsymbols wird das letztere immer noch mit Hilfe des globalen Artinschen Reziprozitätsgesetzes definiert. Erst später, im Frühjahr 1932, gelang Hasse eine rein lokale Definition; er hat sie in seiner Arbeit [Has33a] publiziert, die er Emmy Noether aus Anlass ihres 50.Geburtstages am 23.März 1932 gewidmet hatte. Die Widmung für Emmy Noether war u.a. damit begründet, dass sie seit einer Reihe von Jahren dafür plädiert hatte, die Normenresttheorie rein lokal mit Hilfe der Algebrentheorie aufzubauen, was dann Hasse schließlich auch gelang.¹³¹

Die von Artin erwähnte Formel

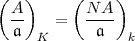(34)

für das m-te Potenzrestsymbol bezieht sich auf eine Körpererweiterung K von k. Es wird vorausgesetzt, dass die m-ten Einheitswurzeln in k liegen. Auf der linken Seite ist das Potenzrestsymbol (Jacobisches Symbol) in K zu nehmen, auf der rechten Seite in k. Und NA bezeichnet die Norm von A K^× nach k. Diese Formel erscheint in §14,2 des Klassenkörperberichts II. Wenn Artin von der „-Formulierung“ spricht, so meint er offenbar eine entsprechende Formel für das Normsymbol. Diese findet sich in §6,3 des Klassenkörperberichts II. Es scheint, dass Hasse den Beweis dieser Formeln und ihren Zusammenhang zum Zeitpunkt des vorliegenden Briefes noch nicht gefunden hatte, und dass er daher Artin danach gefragt hatte. Beim Beweis macht es einige Schwierigkeiten, zu zeigen: wenn in (34) die linke Seite definiert ist, dann ist es auch die rechte Seite. Dazu benötigt Hasse ein von ihm vorher abgeleitetes Primäritätskriterium. Vielleicht ist das der Grund, weshalb Artin schreibt, er sei „ratlos“, weil dieses Kriterium zu dem Zeitpunkt des Briefes noch nicht bekannt war.