Tensor Categories and Representation Theory

Seminar at the HU Berlin / Summer Term 2017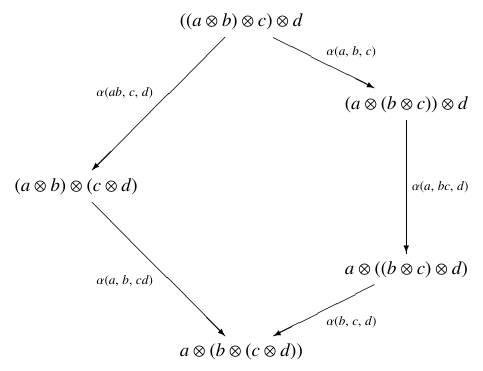

Date and Venue

The seminar usually takes place on

Friday

15 - 17 h

Room 1.113 / RUD25

At some Fridays we may start earlier and have a double session from 13-17 h, to make up for cancellation due to BMS talks on other Fridays.

Seminar Topics

=> For more details see TensorCategories.pdf

Many problems in algebra, geometry and topology lead to tensor categories, i.e. categories equipped with a product that behaves similarly to the tensor product of vector spaces. After a general introduction to such categories, we will discuss a particularly important example: The category of linear representations of an algebraic group. We will see that the group is essentially determined by its representation category, and develop general criteria to decide when a given tensor category is equivalent to one of this form. This Tannaka duality builds a bridge between representation theory and areas such as algebraic geometry and Hodge theory, and if time permits, we may discuss some applications.

Prerequisites

The seminar only requires some basic knowledge about groups and modules over commutative rings, we do not assume any algebraic geometry. The basics of category theory will be recalled or developed as needed.

Selected Literature

1. P. Deligne, J. S. Milne,
   Tannakian Categories,
   LNM 900, Springer (1982) [www]
2. P. Etingof et al.,
   Tensor Categories,
   Math. Surveys and Monographs 205, AMS (2015) [www]
3. W. C. Waterhouse,
   Introduction to Affine Group Schemes,
   GTM 66, Springer (1979) [HU]